题目内容
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的虚半轴长为1,离心率e=$\frac{2\sqrt{3}}{3}$,左、右焦点分别为F1,F2.(1)求双曲线的标准方程;
(2)若过右焦点F2作垂直于x轴的直线1,交双曲线于A、B两点,求|AB|的长.
分析 (1)运用离心率公式和a,b,c的关系,解方程可得a,c,进而得到双曲线的方程;
(2)求得直线l的方程,代入双曲线的方程,求得A,B的坐标,进而得到AB的长.
解答 解:(1)由题意可得,b=1,e=$\frac{c}{a}$=$\frac{2\sqrt{3}}{3}$,
又a2+b2=c2,解得a=$\sqrt{3}$,c=2,
则双曲线的方程为$\frac{{x}^{2}}{3}$-y2=1;
(2)右焦点F2(2,0),
过右焦点F2作垂直于x轴的直线1:x=2,
代入双曲线的方程,可得:
y2=$\frac{1}{3}$,解得y=±$\frac{\sqrt{3}}{3}$.
即有|AB|=$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的方程和性质,考查弦长的求法,注意联立直线和双曲线的方程,考查运算能力,属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
4.2008年5月12日,四川汶川地区发生里氏8.0级特大地震.在随后的几天中,地震专家对汶川地区发生的余震进行了监测.记录的部分数据如下表:
(注:地震强度是指地震时释放的能量)
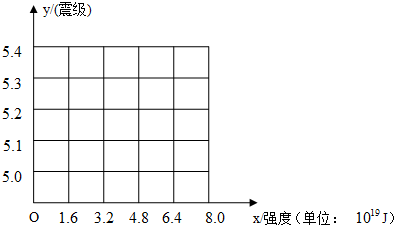
(1)画出震级(y)随地震强度(x)的变化散点图;
(2)根据散点图,从函数y=kx+b,y=algx+b,y=a•10x+b中选取一个函数描述震级y随地震强度x的变化关系;
(3)四川汶川地区发生里氏8.0级特大地震时释放的能量约是多少?(取lg2=0.3)
| 强度(J) | 1.6×1019 | 3.2×1019 | 4.5×1019 | 6.4×1019 |
| 震级(里氏) | 5.0 | 5.2 | 5.3 | 5.4 |
(1)画出震级(y)随地震强度(x)的变化散点图;

(2)根据散点图,从函数y=kx+b,y=algx+b,y=a•10x+b中选取一个函数描述震级y随地震强度x的变化关系;
(3)四川汶川地区发生里氏8.0级特大地震时释放的能量约是多少?(取lg2=0.3)
5.下列关系中,具有相关关系的是( )
(1)名师出高徒; (2)球的体积与该球的半径之间的关系;(3)苹果的产量与气候之间的关系;(4)身高与体重之间的关系;(5)出租车费与行驶的里程;(6)乌鸦叫,没好兆.
(1)名师出高徒; (2)球的体积与该球的半径之间的关系;(3)苹果的产量与气候之间的关系;(4)身高与体重之间的关系;(5)出租车费与行驶的里程;(6)乌鸦叫,没好兆.
| A. | (1)(3)(4) | B. | (1)(2)(4) | C. | (2)(5)(6) | D. | (3)(4)(5) |
2.关于x的不等式kx2-2x+1>0的解集是{x∈R|x≠$\frac{1}{k}$},则k的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | -1≤k≤1 |
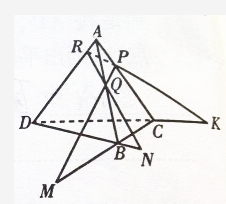 在四面体ABCD中,作截面PQR.若PQ,CB的延长线交于点M,RQ,DB的延长线交于点N,RP,DC的延长线交于点K.求证:M,N,K三点共线.
在四面体ABCD中,作截面PQR.若PQ,CB的延长线交于点M,RQ,DB的延长线交于点N,RP,DC的延长线交于点K.求证:M,N,K三点共线.