题目内容
【题目】如图，在四棱锥P－ABCD中，底面ABCD是菱形，∠ABC＝60°，
为正三角形，且侧面PAB⊥底面ABCD. E，M分别为线段AB，PD的中点.
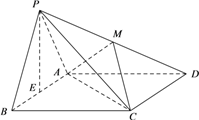
（I）求证：PE⊥平面ABCD；
（II）求证：PB//平面ACM；
（III）在棱CD上是否存在点G，使平面GAM⊥平面ABCD，请说明理由．
【答案】（1）见解析；（2）见解析；（3）见解析.
【解析】试题分析：（1）要证线面垂直，可先证线线垂直，再根据线面垂直的判定得到线面垂直；（2）构造三角形的中位线得到线线平行，进而得到线面平行；（3）在棱CD上存在点G，G为CD的中点时，平面GAM⊥平面ABCD，先猜后证，先证线面垂直，由线面推出面面垂直。解析：
（I）证明：因为
为正三角形，E为AB的中点，
所以PE⊥AB，
又因为面PAB⊥面ABCD，面PAB∩面ABCD=AB， 
平面PAB.
所以PE⊥平面ABCD.
（II）证明：连接BD交AC于H点，连接MH，
因为四边形ABCD是菱形，
所以点H为BD的中点.
又因为M为PD的中点，
所以MH // BP.
又因为 BP 
平面ACM, 
平面ACM.
所以 PB // 平面ACM.
（III）在棱CD上存在点G，G为CD的中点时，平面GAM⊥平面ABCD．
证明：连接
．由（Ⅰ）得，PE⊥平面ABCD，
所以PE⊥CD，因为ABCD是菱形，∠ ABC＝60°，E为AB的中点，
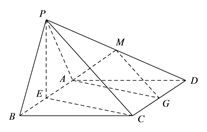
所以
是正三角形，EC⊥AB .
因为CD // AB，
所以EC⊥CD．
因为PE∩EC=E，
所以CD⊥平面PEC，
所以CD⊥PC．
因为M，G分别为PD，CD的中点，
所以MG//PC，
所以CD⊥MG．
因为ABCD是菱形，∠ADC＝60°，
所以
是正三角形.
又因为G为CD的中点，
所以CD⊥AG，
因为MG∩AG=G，
所以CD⊥平面MAG，
因为
平面ABCD，
所以平面MAG⊥平面ABCD．
