Question

【题目】对定义域分别为D1 ， D2的函数y=f（x），y=g（x），规定：函数h（x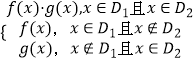）= ，f（x）=x﹣2（x≥1），g（x）=﹣2x+3（x≤2），则h（x）的单调减区间是 ．

Answer 1

【答案】（﹣∞，1），[ ，2]
【解析】解：由题意，函数h（x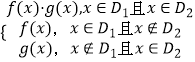）= ， ∵f（x）=x﹣2（x≥1），g（x）=﹣2x+3（x≤2），
∴h（x）的解析式h（x）= ，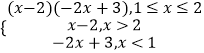
当1≤x≤2时，h（x）=（x﹣2）（﹣2x+3）=﹣2x2+7x﹣6，其对称轴为x= ，
故h（x）在[ ，2]上单调递减，
当x＜1时，h（x）=﹣2x+3为减函数，故减区间为（﹣∞，1），
综上所述h（x）的单调减区间为（﹣∞，1），[ ，2]，
故答案为：（﹣∞，1），[ ，2]
由题中所给的新定义函数，根据其规则结合f（x）=x﹣2（x≥1），g（x）=﹣2x+3（x≤2），直接写出h（x）的解析式即可得到答案．