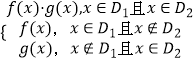题目内容
【题目】已知函数f（x）=loga（x+1），g（x）=loga（4﹣2x），a＞0且a≠1．
（1）求函数y=f（x）﹣g（x）的定义域；
（2）求使不等式f（x）＞g（x）成立的实数x的取值范围；
（3）求函数y=2f（x）﹣g（x）﹣f（1）的零点．
【答案】
（1）
解：y=f（x）﹣g（x）=loga（x+1）﹣loga（4﹣2x），
由题意得： 
，解得：﹣1＜x＜2，
故函数的定义域是（﹣1，2）
（2）
解：不等式f（x）＞g（x），
即loga（x+1）＞loga（4﹣2x），
0＜a＜1时，x+1＜4﹣2x，解得：x＜1，
而﹣1＜x＜2，故不等式的解集是（﹣1，1）；
a＞1时，x+1＞4﹣2x，解得：x＞1，
而﹣1＜x＜2，故不等式的解集是（1，2）；
综上，0＜a＜1时，不等式的解集是（﹣1，1），
a＞1时，不等式的解集是（1，2）
（3）
解：令y=2f（x）﹣g（x）﹣f（1）=0，
即2loga（x+1）=loga（4﹣2x）+loga（1+1），
故（x+1）2=2（4﹣2x），解得：x=﹣7或x=1，
而﹣1＜x＜2，
故x=1．
【解析】（1）根据对数函数的性质求出函数的定义域即可；（2）通过讨论a的范围，得到关于x的不等式，求出不等式的解集即可；（3）令y=0，得到关于x的方程，解出即可．
【考点精析】关于本题考查的对数函数的定义域，需要了解对数函数的定义域范围:（0，+∞）才能得出正确答案．
练习册系列答案
相关题目
