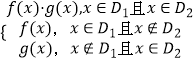Question

【题目】设奇函数定义在上，其导函数为且，当时， ，则不等式的解集为（ ）

A. B.

C. D.

Answer 1

【答案】A

【解析】设g（x）= ，

∴g′（x）

∵f（x）是定义在（﹣π，0）∪（0，π）上的奇函数，

故g（﹣x）===g（x）

∴g（x）是定义在（﹣π，0）∪（0，π）上的偶函数．

∵当0＜x＜π时，f′（x）sinx﹣f（x）cosx＜0

∴g'（x）＜0，

∴g（x）在（0，π）上单调递减，

∴g（x）在（﹣π，0）上单调递增．

∵f（）=0，

∴g（）==0，

∵f（x）＜2f（）sinx，

即g（）sinx＞f（x）；

①当sinx＞0时，即x∈（0，π），g（）＞=g（x）；

所以x∈（，π）；

②当sinx＜0时，即x∈（﹣π，0）时，g（）=g（﹣）＜=g（x）；

所以x∈（﹣，0）；

不等式f（x）＜2f（）sinx的解集为解集为（﹣，0）∪（，π）．

故答案为：（﹣，0）∪（，π）

故答案为A。