题目内容
10.已知关于x的方程$\frac{lg(x-a)}{lgx-lg3}$=2.(1)当a=1时,解此方程;
(2)若方程仅有一个实数解,求a的取值的范围,并求此解.
分析 (1)当a=1时,方程$\frac{lg(x-1)}{lgx-lg3}$=2可化为x-1=$\frac{{x}^{2}}{9}$,解得答案;
(2)方程$\frac{lg(x-a)}{lgx-lg3}$=2可化为$\frac{{x}^{2}}{9}$-x+a=0,结合原式中x>0,x>a,x≠3,分类讨论满足条件的a的取值的范围,可得答案.
解答 解:(1)当a=1时,方程$\frac{lg(x-1)}{lgx-lg3}$=2可化为:lg(x-1)=2lgx-2lg3=lg$\frac{{x}^{2}}{9}$,
则x-1=$\frac{{x}^{2}}{9}$,
解得:x=$\frac{9+3\sqrt{5}}{2}$,或x=$\frac{9-3\sqrt{5}}{2}$
(2)方程$\frac{lg(x-a)}{lgx-lg3}$=2可化为:lg(x-a)=2lgx-2lg3=lg$\frac{{x}^{2}}{9}$,
即x-a=$\frac{{x}^{2}}{9}$,即$\frac{{x}^{2}}{9}$-x+a=0.
若x=3,满足$\frac{{x}^{2}}{9}$-x+a=0,则a=2,此时方程$\frac{{x}^{2}}{9}$-x+2=0还有另一解x=6满足条件;
若a<0,则方程$\frac{{x}^{2}}{9}$-x+a=0两根异号,其中负根不能做为真数舍去,另一解为:x=$\frac{9+3\sqrt{9-4a}}{2}$,满足条件;
若a=0,则方程$\frac{{x}^{2}}{9}$-x=0有两根,x=9,x=0,其中0不能做为真数舍去,满足条件;
若a=$\frac{9}{4}$,则方程$\frac{{x}^{2}}{9}$-x+a=0有两等根,x=$\frac{9}{2}$,满足条件;
若0<a<$\frac{9}{4}$,且a≠2,则方程$\frac{{x}^{2}}{9}$-x+a=0有两相异正根,均满足原方程不合题意;
若a>$\frac{9}{4}$,则方程$\frac{{x}^{2}}{9}$-x+a=0无解,则原方程也无解不合题意;
综上所述,a≤0,或a=$\frac{9}{4}$,或a=2
点评 本题考查的知识点是对数方程的解法,分类讨论思想,难度较大,分类复杂.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | 2$\sqrt{2}$+3 | C. | 2$\sqrt{2}$ | D. | 3一2$\sqrt{2}$ |
| A. | $log_4^{0.3}<{0.4^3}<{3^{0.4}}$ | B. | ${0.4^3}<log_4^{0.3}<{3^{0.4}}$ | ||
| C. | $log_4^{0.3}<{3^{0.4}}<{0.4^3}$ | D. | ${0.4^3}<{3^{0.4}}<log_4^{0.3}$ |
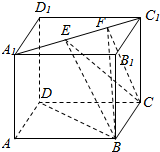 如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )| A. | BD⊥CE | |
| B. | △CEF的面积为定值 | |
| C. | 四面体BCEF的体积随EF的位置的变化而变化 | |
| D. | 直线BE与CF为异面直线 |