题目内容
已知关于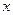
的一元二次方程
，求使方程有两个大于零的实数根的充要条件
解：设x1，x2是方程的两根，则原方程的两个根都大于0的等价条件是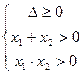
即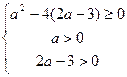
解得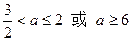 
∴a的取值范围是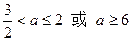
解析
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
应用题天天练四川大学出版社系列答案题目内容
已知关于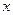的一元二次方程，求使方程有两个大于零的实数根的充要条件
解：设x1，x2是方程的两根，则原方程的两个根都大于0的等价条件是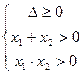 即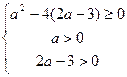
解得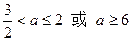
∴a的取值范围是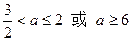
解析
应用题天天练四川大学出版社系列答案
是偶函数．
的值;
,若函数
与
的图象有且只有一个公共点,求
的取值范围． 
在
上是增函数；
在
上的值域。
，且
.
的奇偶性并说明理由； 
上的单调性，并证明你的结论；
上，不等式
恒成立，试确定实数
的取值范围.
和
的图像的示意图如图所示， 两函数的图像在第一象限只有两个交点
，
，
，
分别对应哪一个函数；（4分）
的大小，并按从小到大的顺序排列；（5分）
,则函数
的两个零点为
，如果
，
，其中
为整数，指出
，
的值，并说明理由； （5分）
，常数
.
，判断
在区间
上的单调性，并加以证明；
的取值范围.
，在
时的图象是如图所示的抛物线的一部分，
≤（
）x－2，求函数y=2x－2－x的值域.
（
）的最大值为1，对任意
，有
。
的解析式；
，其中
，求
的值。