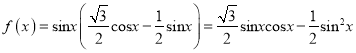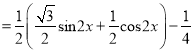Question

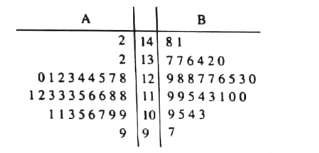
【题目】广场舞是现代城市群众文化、娱乐发展的产物，其兼具文化性和社会性，是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查，随机抽取了40名广场舞者进行调查，将他们年龄分成6段：[20，30），[30，40），[40，50），[50，60），[60，70），[70，80]后得到如图所示的频率分布直方图．

（1）估计在40名广场舞者中年龄分布在[40，70）的人数；
（2）求40名广场舞者年龄的中位数和平均数的估计值；
（3）若从年龄在[20，40）中的广场舞者中任取2名，求这两名广场舞者年龄在[30，40）中的人数X的分布列及数学期望．

Answer 1

【答案】
（1）解：由频率分布直方图得年龄分布在[40，70）的频率为（0.020+0.030+0.025）×10=0.75，

∴在40名广场舞者中年龄分布在[40，70）的人数为：40×0.75=30（人）

（2）解：年龄分布在[20，50）的频率为（0.005+0.010+0.020）×10=0.35，

年龄分布在[50，60）的频率为0.3，

∴中位数为：50+ =55．

平均数的估计值为：25×0.05+35×0.1+45×0.2+55×0.3+65×0.25+75×0.1=54

（3）解：从年龄在[20，40）中的广场舞者有（0.005+0.010）×10×40=6人，

其中年龄在[20，30）中的广场舞者有2人，年龄在[30，40）中的广场舞者有4人，

∴X的可能取值为0，1，2，

P（X=0）= = ，

P（X=1）= = ，

P（X=2）= = ，

∴X的分布列为：

X	0	1	2
P

EX= =

【解析】（1）由频率分布直方图先求出年龄分布在[40，70）的频率，由此能求出在40名广场舞者中年龄分布在[40，70）的人数．（2）利用频率分布图能求出40名广场舞者年龄的中位数和平均数的估计值．（3）从年龄在[20，40）中的广场舞者有6人，其中年龄在[20，30）中的广场舞者有2人，年龄在[30，40）中的广场舞者有4人，X的可能取值为0，1，2，分别求出相应的概率，由此能求出X的分布列和EX．
【考点精析】根据题目的已知条件，利用频率分布直方图和离散型随机变量及其分布列的相关知识可以得到问题的答案，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．