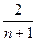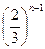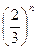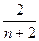题目内容
(本小题满分14分)
各项均为正数的数列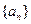 ,
,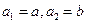 ,且对满足
,且对满足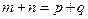 的正整数
的正整数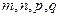 都有
都有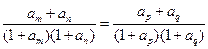 。
。
(1)当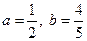 时,求通项
时,求通项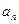 ;
;
(2)证明:对任意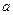 ,存在与
,存在与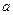 有关的常数
有关的常数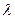 ,使得对于每个正整数
,使得对于每个正整数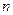 ,都有
,都有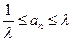 。
。
各项均为正数的数列
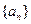 ,
,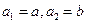 ,且对满足
,且对满足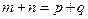 的正整数
的正整数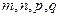 都有
都有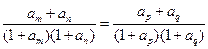 。
。(1)当
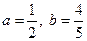 时,求通项
时,求通项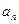 ;
;(2)证明:对任意
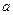 ,存在与
,存在与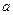 有关的常数
有关的常数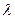 ,使得对于每个正整数
,使得对于每个正整数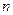 ,都有
,都有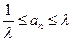 。
。(1)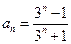
(2)证明见解析。
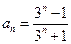
(2)证明见解析。
(1)由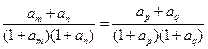 得
得
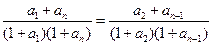 ,将
,将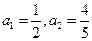 代入化简得
代入化简得
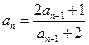 。
。
所以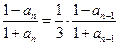 ,
,
故数列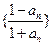 为等比数列,从而
为等比数列,从而
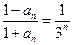 ,即
,即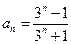 。
。
可验证,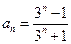 满足题设条件。
满足题设条件。
(2)由题设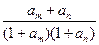 的值仅与
的值仅与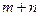 有关,记为
有关,记为 则
则
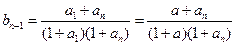 。
。
考察函数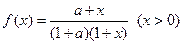 ,则在定义域上有
,则在定义域上有
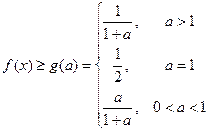
故对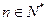 ,
,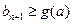 恒成立。
恒成立。
又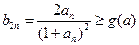 ,
,
注意到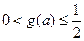 ,解上式得
,解上式得
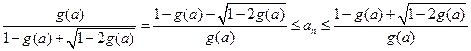 ,
,
取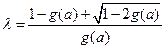 ,即有
,即有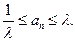 。
。
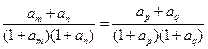 得
得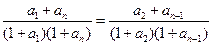 ,将
,将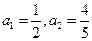 代入化简得
代入化简得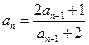 。
。所以
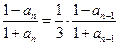 ,
,故数列
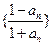 为等比数列,从而
为等比数列,从而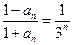 ,即
,即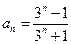 。
。可验证,
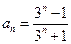 满足题设条件。
满足题设条件。(2)由题设
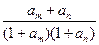 的值仅与
的值仅与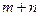 有关,记为
有关,记为 则
则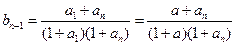 。
。考察函数
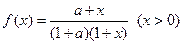 ,则在定义域上有
,则在定义域上有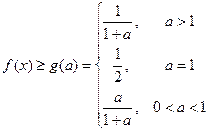
故对
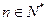 ,
,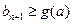 恒成立。
恒成立。又
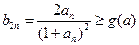 ,
,注意到
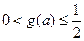 ,解上式得
,解上式得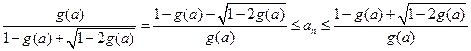 ,
,取
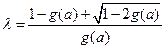 ,即有
,即有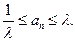 。
。
练习册系列答案
相关题目
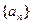 ,
,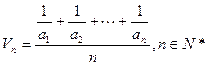 。
。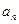 }的倒均数是
}的倒均数是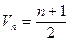 ,求数列{
,求数列{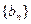 的首项为-1,公比为
的首项为-1,公比为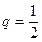 ,其倒数均为
,其倒数均为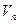 ,若存在正整数k,使得当
,若存在正整数k,使得当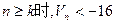 恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)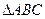 中,已知角A、B、C成等差数列,且
中,已知角A、B、C成等差数列,且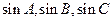 成等比数列,则
成等比数列,则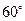 的不等边三角形 D.等比三角形
的不等边三角形 D.等比三角形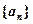 中,
中,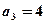 ,且
,且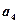 ,
,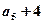 ,
,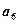 成等差数列.
成等差数列.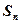 ,求
,求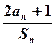 的最大值.
的最大值.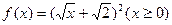 ,数列
,数列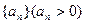 的前
的前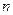 项和
项和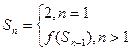
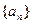 的通项公式;
的通项公式;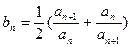 ,
,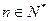 ,求
,求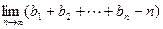 的值.
的值.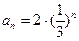 ,把数列
,把数列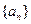 的各项排成三角形状:
的各项排成三角形状: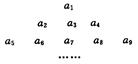
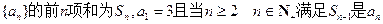 与—3的等差中项。(1)求
与—3的等差中项。(1)求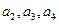 ;(2)求数列
;(2)求数列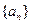 的通项公式。
的通项公式。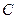 :
: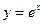 (其中
(其中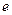 为自然对数的底数)在点
为自然对数的底数)在点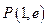 处的切线与
处的切线与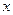 轴交于点
轴交于点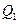 ,过点
,过点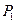 ,曲线
,曲线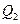 ,过点
,过点 于点
于点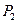 ,……,依次下去得到一系列点
,……,依次下去得到一系列点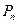 ,设点
,设点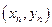 (
(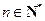 ).(Ⅰ)分别求
).(Ⅰ)分别求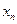 与
与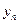 的表达式;(Ⅱ)设O为坐标原点,求
的表达式;(Ⅱ)设O为坐标原点,求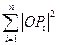
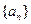 满足
满足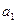 ="1,"
="1," 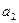 =
=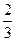 ,且
,且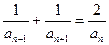 (n≥2),
(n≥2),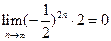 则
则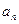 等于( )
等于( )