题目内容
14.求下列数列的通式:(1)1,$\frac{1}{3}$,$\frac{9}{35}$,$\frac{17}{63}$,$\frac{33}{99}$,…
(2)$\frac{4}{5}$,-1,$\frac{10}{17}$,-$\frac{13}{31}$,$\frac{16}{65}$,…
分析 根据数列项的特点,找出规律性即可得到结论.
解答 解:(1)1,$\frac{1}{3}$,$\frac{9}{35}$,$\frac{17}{63}$,$\frac{33}{99}$,…
等价为$\frac{3}{3}$,$\frac{5}{15}$,$\frac{9}{35}$,$\frac{17}{63}$,$\frac{33}{99}$,…
即$\frac{1+{2}^{1}}{{2}^{2}-1}$,$\frac{1+{2}^{2}}{{4}^{2}-1}$,$\frac{1+{2}^{3}}{{6}^{2}-1}$,$\frac{1+{2}^{4}}{{8}^{2}-1}$,$\frac{1+{2}^{5}}{1{0}^{2}-1}$.
则对应的通项公式为an=$\frac{1+{2}^{n}}{(2n)^{2}-1}$.
(2)$\frac{4}{5}$,-1,$\frac{10}{17}$,-$\frac{13}{31}$,$\frac{16}{65}$,…
等价为$\frac{4}{5}$,-$\frac{7}{7}$,$\frac{10}{17}$,-$\frac{13}{31}$,$\frac{16}{65}$,
即$\frac{4}{4+1}$,-$\frac{4+3}{8-1}$,$\frac{4+3×2}{16+1}$,-$\frac{4+3×3}{32-1}$,$\frac{4+3×4}{64+1}$,
即$\frac{4}{{2}^{2}+1}$,-$\frac{4+3}{{2}^{3}-1}$,$\frac{4+3×2}{{2}^{4}+1}$,-$\frac{4+3×3}{{2}^{5}-1}$,$\frac{4+3×4}{{2}^{6}+1}$,
故数列的一个通项公式为an=$\frac{4+3(n-1)}{{2}^{n+1}+(-1)^{n+1}}$.
点评 本题主要考查数列的通项公式的求解,根据数列项的规律是解决本题的关键.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案| A. | -1或2 | B. | 1或-2 | C. | -1或-2 | D. | 1或2 |
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,+∞) |
| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 无法判断 |
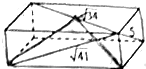 如图,已知长方体过一个顶点的三条面对角线的长分别为5,$\sqrt{34}$,$\sqrt{41}$,则其外接球(长方体的顶点均在球面上)的表面积是50π.
如图,已知长方体过一个顶点的三条面对角线的长分别为5,$\sqrt{34}$,$\sqrt{41}$,则其外接球(长方体的顶点均在球面上)的表面积是50π.