题目内容
【题目】已知函数f(x)=x2﹣4|x|+3,x∈R.
(1)判断函数的奇偶性并将函数写成分段函数的形式;
(2)画出函数的图象,根据图象写出它的单调区间; 
(3)若函数f(x)的图象与y=a的图象有四个不同交点,则实数a的取值范围.
【答案】
(1)解:因为函数的定义域为R,关于坐标原点对称,
且f(﹣x)=(﹣x)2﹣4|﹣x|+3=x2﹣4|x|+3=f(x),
故函数为偶函数.
f(x)=x2﹣4|x|+3= ![]()
(2)解:如图,
单调增区间为::[﹣2,0),[2,+∞),
单调减区间为(﹣∞,﹣2),[0,2]
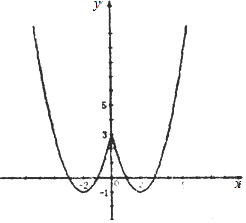
(3)解:由函数的图象可知:函数f(x)的图象与y=a的图象有四个不同交点,则实数a的取值范围:(﹣1,3)
【解析】(1)由f(﹣x)=f(x)得函数为偶函数,对x分类讨论:x≥0,x<0得分段函数的解析式;(2)由分段函数分两种情况作二次函数的图象;(3)由图象可知函数的单调区间及值域.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

