题目内容
【题目】已知函数f(x)=lnx﹣ ![]() ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
(1)求函数f(x)的极值;
(2)在曲线y=f(x)的图象上是否存在不同的两点A(x1 , y1),B(x2 , y2)(x1≠x2),使得直线AB的斜率k=f′( ![]() )?若存在,求出x1与x2的关系;若不存在,请说明理由.
)?若存在,求出x1与x2的关系;若不存在,请说明理由.
【答案】
(1)解:由已知得,f′(x)= ![]() (1)当a≤0时,∵x>0,∴f′(x)>0;
(1)当a≤0时,∵x>0,∴f′(x)>0;
∴f(x)在(0,+∞)上是增函数,此时函数f(x)无极值;(2)当a>0时, ![]() ;
;
∴当x ![]() 时,g′(x)>0;当x
时,g′(x)>0;当x ![]() 时,g′(x)<0;
时,g′(x)<0;
∴函数f(x)在 ![]() 上是增函数,在
上是增函数,在 ![]() 上是减函数;
上是减函数;
∴当 ![]() 时,f(x)有极大值
时,f(x)有极大值 ![]() ,无极小值;
,无极小值;
综上所述,当a≤0时,函数f(x)无极值,当a>0时,f(x)有极大值 ![]() ,无极小值.
,无极小值.
(2)解:由题意得,
![]() =
= 
=  =
= 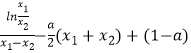 .
.
![]() .
.
由 ![]() 得,
得, 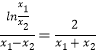 ;
;
即 ![]() ,即
,即 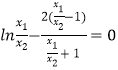 ;
;
令 ![]() ,不妨设x1>x2,则t>1,记
,不妨设x1>x2,则t>1,记 ![]() ;
;
![]() ,所以g(t)在(1,+∞)上是增函数;
,所以g(t)在(1,+∞)上是增函数;
所以g(t)>g(1)=0,所以方程g(t)=0无解,则满足条件的两点A,B不存在.
【解析】(1)求导数 ![]() ,讨论a的符号,这样便可判断导数的符号,从而可判断每种情况是否存在极值,若存在便可求出该极值;(2)先根据条件求出斜率
,讨论a的符号,这样便可判断导数的符号,从而可判断每种情况是否存在极值,若存在便可求出该极值;(2)先根据条件求出斜率 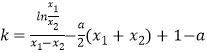 ,而可得到
,而可得到 ![]() ,这样便可根据条件得出
,这样便可根据条件得出 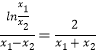 ,然后换元
,然后换元 ![]() ,并设x1>x2 , t>1,从而得出
,并设x1>x2 , t>1,从而得出 ![]() ;求导数并可判断导数符号g′(t)>0,从而g(t)>g(1),而g(1)=0,这即说明g(t)=0无解,从而得出满足条件的两点A,B不存在.
;求导数并可判断导数符号g′(t)>0,从而g(t)>g(1),而g(1)=0,这即说明g(t)=0无解,从而得出满足条件的两点A,B不存在.
【考点精析】认真审题,首先需要了解函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值).
是极小值).

 阅读快车系列答案
阅读快车系列答案