题目内容
.若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,
则这个数列有 ( )
则这个数列有 ( )
| A.13项 | B.12项 | C.11项 | D.10项 |
A
先根据题意求出a1+an的值,再把这个值代入求和公式,进而求出数列的项数n.
解答:解:依题意a1+a2+a3=34,an+an-1+an-2=146
∴a1+a2+a3+an+an-1+an-2=34+146=180
又∵a1+an=a2+an-1=a3+++an-2
∴a1+an=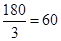
∴Sn=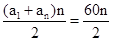 =390
=390
∴n=13
故选A
解答:解:依题意a1+a2+a3=34,an+an-1+an-2=146
∴a1+a2+a3+an+an-1+an-2=34+146=180
又∵a1+an=a2+an-1=a3+++an-2
∴a1+an=
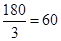
∴Sn=
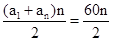 =390
=390∴n=13
故选A

练习册系列答案
相关题目
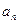 }和{
}和{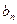 }满足:对于任何
}满足:对于任何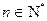 ,有
,有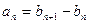 ,
,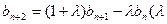 为非零常数),且
为非零常数),且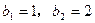 .
.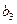 是
是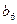 与
与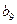 的等差中项,试求
的等差中项,试求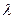 的值,并研究:对任意的
的值,并研究:对任意的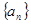 的前n项和为
的前n项和为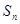 ,若
,若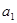 =11,且
=11,且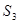 =27,则当
=27,则当 前n项和Sn;
前n项和Sn;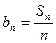 ,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
,求证:数列{bn}中任意不同的三项都不可能成为等比数列.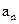 ﹜中,
﹜中, =
=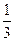 ,前n项和
,前n项和 满足
满足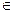 N*
N* )
)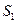 ,t(
,t(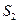 ), 3(
), 3(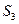 )成等差数列,求实数t的值。
)成等差数列,求实数t的值。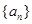 的前20项的和为100,那么
的前20项的和为100,那么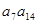 的最大值为
的最大值为 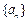 的前n项和为
的前n项和为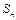 ,且
,且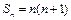 (
(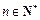 ).
).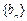 满足:
满足: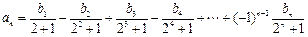 (
(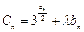 (
(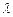 ,使
,使 得当
得当 恒成立?若存在,求出实数
恒成立?若存在,求出实数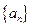 前
前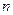 项和为
项和为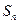 ,点
,点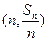
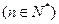 均在函数
均在函数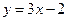 图象上。
图象上。 项公式;
项公式;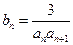 ,
, 是数列
是数列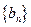 的前
的前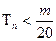 对所有
对所有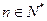 都成立的最小正整数
都成立的最小正整数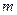 。
。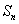 是公差不为0的等差数列
是公差不为0的等差数列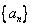 的前
的前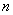 项和,且
项和,且 、
、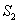 、
、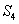 成等比数列。
成等比数列。 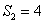 ,求:数列
,求:数列