题目内容
9.若定义在区间[-2015,2015]上的函数f(x)满足:对于任意的x1,x2∈[-2015,2015],都有f(x1+x2)=f(x1)+f(x2)-2015,且x>0时,有f(x)<2015,f(x)的最大值、最小值分别为M,N,则M+N的值为( )| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
分析 根据抽象函数的表达式,利用函数单调性的性质即可得到结论.
解答 解:∵对于任意的x1,x2∈[-2015,2015],都有f(x1+x2)=f(x1)+f(x2)-2015,
∴令x1=x2=0,得f(0)=2015,
再令x1+x2=0,将f(0)=2015代入可得f(x)+f(-x)=4030.
设x1<x2,x1,x2∈[-2015,2015],
则x2-x1>0,f(x2-x1)=f(x2)+f(-x1)-2015,
∴f(x2)+f(-x1)-2015<2015.
又∵f(-x1)=4030-f(x1),
∴可得f(x2)>f(x1),
即函数f(x)是递减的,
∴f(x)max=f(-2015),f(x)min=f(2015).
又∵f(2015)+f(-2015)=4030,
∴M+N的值为4030.
故选:D.
点评 本题主要考查函数值的计算,利用赋值法,证明函数的单调性是解决本题的关键,综合性较强,有一定的难度.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
17.某校计划用系统抽样方法从高一年级500名学生中抽取25名进行调查.首先将这500名学生编号,号码为1~500;接着随机抽取一个号码,抽到的是5号,则本次抽样还将抽到的学生号码是( )
| A. | 15 | B. | 25 | C. | 35 | D. | 50 |
14.已知f(x)=3x+3-x,若f(a)=4,则f(2a)=( )
| A. | 4 | B. | 14 | C. | 16 | D. | 18 |
1.已知p:(x+3)(x+4)=0,q:x+3=0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
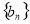 与数列
与数列
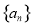 满足
满足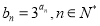
 是何种数列,并给出证明;
是何种数列,并给出证明;
 =( )
=( ) D.(﹣2,0)
D.(﹣2,0)