题目内容
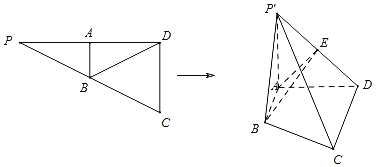
【题目】在三棱锥![]() 中,
中,![]() ,二面角
,二面角![]() 、
、![]() 、
、![]() 的大小均为
的大小均为![]() ,设三棱锥
,设三棱锥![]() 的外接球球心为
的外接球球心为![]() ,直线
,直线![]() 交平面
交平面![]() 于点
于点![]() ,则三棱锥
,则三棱锥![]() 的内切球半径为_______________,
的内切球半径为_______________,![]() __________
__________
【答案】![]()
![]()
【解析】
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,则由已知
,则由已知![]() 是
是![]() 内心,由直角三角形的性质求得内切圆半径从而可得
内心,由直角三角形的性质求得内切圆半径从而可得![]() ,由此用体积法求得内切球半径,过斜边中点
,由此用体积法求得内切球半径,过斜边中点![]() 作平面
作平面![]() 的垂线,则外接球球心在此垂线上,只是要确定在平面
的垂线,则外接球球心在此垂线上,只是要确定在平面![]() 的哪一侧,可分类讨论,同时由垂直得平行,从而得
的哪一侧,可分类讨论,同时由垂直得平行,从而得![]() 共线,求出外接球半径,求得
共线,求出外接球半径,求得![]() 后可得结论.
后可得结论.
如图,作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,过
,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,由
,由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,得
,得![]() ,同理
,同理![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角,所以
的平面角,所以![]() ,所以
,所以![]() ,
,
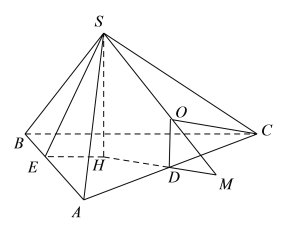
图1
又面角![]() 、
、![]() 、
、![]() 的大小均为
的大小均为![]() ,所以
,所以![]() 到
到![]() 三边距离相等,
三边距离相等,![]() 点到
点到![]() 的距离也相等,所以
的距离也相等,所以![]() 是
是![]() 的内心,
的内心,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,从而
,从而![]() ,
,![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
所以三棱锥![]() 的全面积为
的全面积为![]() ,
,
设内切球半径为![]() ,则
,则![]() ,所以
,所以![]() .
.
设![]() 是
是![]() 中点,则
中点,则![]() 是
是![]() 外心,所以
外心,所以![]() 平面
平面![]() ,所以
,所以![]() ,则
,则![]() 共线,
共线,
在直角![]() 中,以
中,以![]() 为
为![]() 轴建立平面直角坐标系,由
轴建立平面直角坐标系,由![]() ,
,![]() ,∴
,∴![]() ,
,
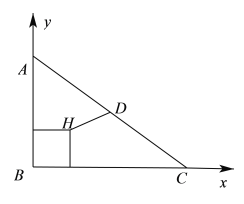
设三棱锥![]() 外接球半径为
外接球半径为![]() ,即
,即![]() ,若
,若![]() 在图1位置所示,由直角梯形
在图1位置所示,由直角梯形![]() 和直角
和直角![]() 得
得![]() (*),解得
(*),解得![]() 与(*)式不合,
与(*)式不合,
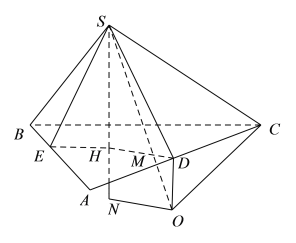
图2
若![]() 如图2位置所示,则
如图2位置所示,则![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
∴![]() ,∴
,∴![]() .
.
故答案为:![]() ;
;![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目