题目内容
【题目】我国是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)若全市居民中月均用水量不低于3吨的人数为3.6万,试估计全市有多少居民?并说明理由;
(Ⅱ)若该市政府拟采取分层抽样的方法在用水量吨数为![]() 和
和![]() 之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设
之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖的家庭数,
中的获奖的家庭数,![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖家庭数,记随机变量
中的获奖家庭数,记随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(Ⅰ)30万;(Ⅱ)![]() .
.
【解析】
(1)由图,不低于3吨人数所占百分比为![]() ,解出即可得出.
,解出即可得出.
(2)由概率统计相关知识,各组频率之和的值为1,频率![]()
![]() ,,可得
,,可得![]() ,得a
,得a![]() .据题意可知随机变量
.据题意可知随机变量![]() 的取值为0,2,4.利用相互独立、互斥事件的概率计算公式即可得出.
的取值为0,2,4.利用相互独立、互斥事件的概率计算公式即可得出.
(Ⅰ)由图,不低于3吨人数所占百分比为![]()
所以假设全市的人数为![]() (万人),则有
(万人),则有![]() ,解得
,解得![]()
所以估计全市人数为30万.
(Ⅱ)由概率统计相关知识,各组频率之和的值为1,因为频率![]()
![]() ,
,
所以![]() ,得
,得![]() ,
,
用水量在![]() 之间的户数为
之间的户数为![]() 户,而用水量在
户,而用水量在![]() 吨之间的户数为
吨之间的户数为![]() 户,根据分层抽样的方法,总共需要抽取7户居民,所以用水量在
户,根据分层抽样的方法,总共需要抽取7户居民,所以用水量在![]() 之间应抽取的户数为
之间应抽取的户数为![]() 户,而用水量在
户,而用水量在![]() 吨之间的户数为
吨之间的户数为![]() 户.
户.
据题意可知随机变量![]() 的取值为0,2,4.
的取值为0,2,4.
![]() ,
,
![]() ,
,
![]() ,
,
其分布列为:
| 0 | 2 | 4 |
|
|
|
|
期望为:![]() .
.

【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
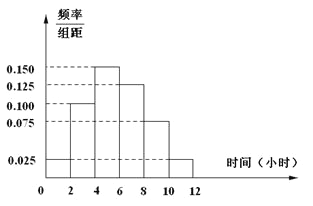
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |