题目内容
1.求函数y=$\sqrt{x}$+$\sqrt{5-x}$的值域.分析 法一:求导数y′=$\frac{\sqrt{5-x}-\sqrt{x}}{2\sqrt{x}•\sqrt{5-x}}$,可判断函数$\sqrt{5-x}-\sqrt{x}$在[0,5]上单调递减,从而可判断导数的符号,从而得出$x=\frac{5}{2}$时,原函数取到最大值,x=0或x=5时,原函数取得最小值,这样即可得出原函数的值域,再一种方法是对原函数式两边平方,求y2的范围,再开方,从而得出原函数的值域.
法二:对函数y=$\sqrt{x}$+$\sqrt{5-x}$的等号两端平方后求得最值,再开方,
解答 解:法一:函数的定义域为[0,5];
$y′=\frac{1}{2\sqrt{x}}-\frac{1}{2\sqrt{5-x}}=\frac{\sqrt{5-x}-\sqrt{x}}{2\sqrt{x}•\sqrt{5-x}}$;
函数y=$\sqrt{5-x}-\sqrt{x}$在[0,5]上为减函数,令$\sqrt{5-x}=\sqrt{x}$,则x=$\frac{5}{2}$;
∴$x∈[0,\frac{5}{2})$时,y′>0,x$∈(\frac{5}{2},5]$时,y′<0;
∴$x=\frac{5}{2}$时,原函数取得最大值$\sqrt{10}$;
又x=0时,y=$\sqrt{5}$,x=5时,y=$\sqrt{5}$;
∴原函数的值域为:$[\sqrt{5},\sqrt{10}]$.
法二:${y}^{2}=(\sqrt{x}+\sqrt{5-x})^{2}=5+2\sqrt{-{x}^{2}+5x}$;
$-{x}^{2}+5x=-(x-\frac{5}{2})^{2}+\frac{25}{4}≤\frac{25}{4}$;
x=0,和5时,-x2+5x=0;
∴$0≤-{x}^{2}+5x≤\frac{25}{4}$;
∴$0≤\sqrt{-{x}^{2}+5x}≤\frac{5}{2}$;
∴5≤y2≤10;
∴$\sqrt{5}≤y≤\sqrt{10}$;
∴原函数的值域为$[\sqrt{5},\sqrt{10}]$.
点评 考查函数值域的概念,根据导数符号判断函数的单调性,以及根据导数求函数最值的方法,以及单调性定义的应用.

| A. | 无解 | B. | 一解 | C. | 两解 | D. | 一解或两解 |
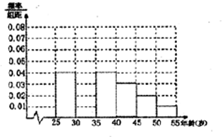 某班同学利用劳动节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
某班同学利用劳动节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55) | 15 | 0.3 |
(2)请根据(1)中补全的频率分布直方图求抽取n的人的年龄的众数和中位数的估计值.