题目内容
6.已知函数f(x)=$\sqrt{3}$sin2x-cos2x.(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调递减区间;
(3)求f(x)在区间[-$\frac{π}{6}$,$\frac{π}{4}$]上的最大值和最小值.
分析 (1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=2sin(2x-$\frac{π}{6}$),利用周期公式即可得解.
(2)由2kπ$+\frac{π}{2}$≤2x-$\frac{π}{6}$$≤2kπ+\frac{3π}{2}$,k∈Z,可解得函数f(x)的单调递减区间.
(3)由x∈[-$\frac{π}{6}$,$\frac{π}{4}$],可求2x-$\frac{π}{6}$∈[-$\frac{π}{2}$,$\frac{π}{3}$],利用正弦函数的图象和性质即可得解.
解答 解:(1)∵f(x)=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$),
∴函数f(x)的最小正周期T=$\frac{2π}{2}=π$.
(2)由2kπ$+\frac{π}{2}$≤2x-$\frac{π}{6}$$≤2kπ+\frac{3π}{2}$,k∈Z,可解得函数f(x)的单调递减区间为:[k$π+\frac{π}{3}$,k$π+\frac{5π}{6}$]k∈Z.
(3)∵x∈[-$\frac{π}{6}$,$\frac{π}{4}$],
∴2x-$\frac{π}{6}$∈[-$\frac{π}{2}$,$\frac{π}{3}$],
∴sin(2x-$\frac{π}{6}$)∈[-1,$\frac{\sqrt{3}}{2}$],
∴f(x)=2sin(2x-$\frac{π}{6}$)在区间[-$\frac{π}{6}$,$\frac{π}{4}$]上的最大值为$\sqrt{3}$,最小值为-2.
点评 本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
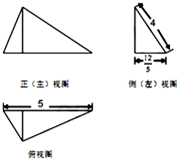
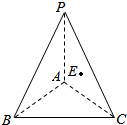 已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,E是点A在平面PBC内的射影,求证:PA⊥平面ABC.
已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,E是点A在平面PBC内的射影,求证:PA⊥平面ABC.