题目内容
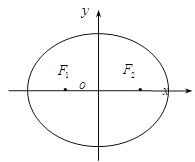
【题目】已知椭圆![]() 上存在关于直线
上存在关于直线![]() 对称的相异两点,则实数
对称的相异两点,则实数![]() 的取值范围是____.
的取值范围是____.
【答案】![]()
【解析】
根据对称性可知线段AB被直线y=x+m垂直平分,且AB的中点M(x0,y0)在直线y=x+m上,故可设直线AB的方程为y=﹣x+b,联立方程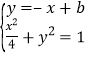 整理可得5x2﹣8bx+4b2﹣4=0,结合方程的根与系数关系可求中点M,由△=64b2﹣80(b2﹣1)>0可求b的范围,由中点M在直线yx+m可得b,m的关系,从而可求m的范围
整理可得5x2﹣8bx+4b2﹣4=0,结合方程的根与系数关系可求中点M,由△=64b2﹣80(b2﹣1)>0可求b的范围,由中点M在直线yx+m可得b,m的关系,从而可求m的范围
设椭圆![]() 上存在关于直线y=x+m对称的两点为A(x1,y1),B(x2,y2)
上存在关于直线y=x+m对称的两点为A(x1,y1),B(x2,y2)
根据对称性可知线段AB被直线y=x+m垂直平分,且AB的中点M(x0,y0)在直线y=x+m上,且KAB=﹣1
故可设直线AB的方程为y=﹣x+b
联立方程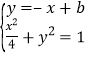 整理可得5x2﹣8bx+4b2﹣4=0
整理可得5x2﹣8bx+4b2﹣4=0
∴![]() ,y1+y2=2b﹣(x1+x2)=
,y1+y2=2b﹣(x1+x2)=![]()
由△=64b2﹣80(b2﹣1)>0可得![]()
∴![]() ,
,![]() =
=![]()
∵AB的中点M(![]() )在直线y=x+m上
)在直线y=x+m上
∴![]() ,
,![]()
∴![]()
故答案为:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目