题目内容
已知四棱锥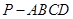 中,
中,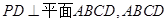 是正方形,E是
是正方形,E是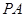 的中点,
的中点,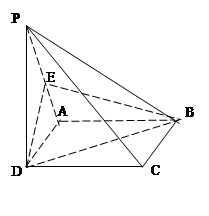
(1)若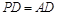 ,求 PC与面AC所成的角
,求 PC与面AC所成的角
(2) 求证: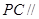 平面
平面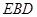
(3) 求证:平面PBC⊥平面PCD
(1) (2)先证明EO∥PC (3)先证明BC^平面PAB
(2)先证明EO∥PC (3)先证明BC^平面PAB
解析试题分析:本题第(1)问,关键是找出PC与面AC所成的角 ,由于
,由于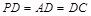 ,则
,则 ;第二问,关键是证明EO∥PC,由于EO是三角形PAC的中位线,则EO∥PC,结合直线与平面平行的判定定理,只要在说明PC
;第二问,关键是证明EO∥PC,由于EO是三角形PAC的中位线,则EO∥PC,结合直线与平面平行的判定定理,只要在说明PC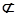 平面EBD,EO
平面EBD,EO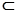 平面EBD,就可以下结论PC∥平面EBD;第(3)问,先证明PD^BC和BC^CD,则BC^平面PAB,又因为BC
平面EBD,就可以下结论PC∥平面EBD;第(3)问,先证明PD^BC和BC^CD,则BC^平面PAB,又因为BC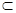 平面PBC,所以就有平面PBC^平面PCD。
平面PBC,所以就有平面PBC^平面PCD。
解:
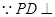 平面
平面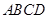 ,
,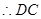 是直线
是直线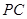 在平面
在平面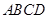 上的射影,
上的射影, 是直线
是直线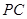 和平面
和平面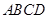 所成的角。又
所成的角。又 ,四边形
,四边形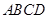 是正方形,
是正方形,
 ,
, ;
; 直线
直线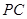 和平面
和平面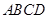 所成的角为
所成的角为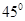
(2)连接AC交BD与O,连接EO, ∵E、O分别为PA、AC的中点
∴EO∥PC ∵PC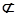 平面EBD,EO
平面EBD,EO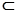 平面EBD ∴PC∥平面EBD
平面EBD ∴PC∥平面EBD
(3)∵PD^平面ABCD, BC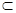 平面ABCD,∴PD^BC,
平面ABCD,∴PD^BC,
∵ABCD为正方形 ∴ BC^CD,
∵PD∩CD="D," PD,CD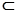 平面PCD
平面PCD
∴BC^平面PCD
又∵ BC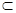 平面PBC,∴平面PBC^平面PCD
平面PBC,∴平面PBC^平面PCD
考点:直线与平面所成的角;直线与平面平行的判定;平面与平面垂直的判定.
点评:本题考查直线和平面平行和垂直关系的判定,直线和平面所成角的计算.考查考查空间想象能力、转化、计算、推理论证能力。

练习册系列答案
相关题目
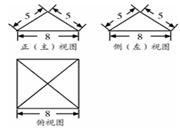
 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.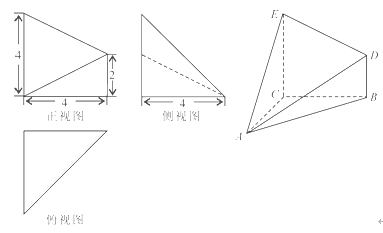
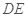 与
与 所成角的余弦值;
所成角的余弦值;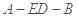 的正弦值;
的正弦值;  中,
中,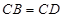 ,
,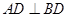 ,点
,点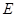 ,
,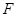 分别是
分别是 ,
, 的中点.
的中点.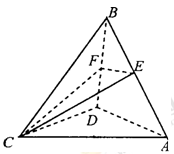
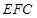 ⊥平面
⊥平面 ;
;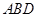 ⊥平面
⊥平面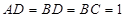 ,求三棱锥
,求三棱锥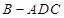 的体积.
的体积.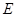 是矩形
是矩形 中
中 边上的点,
边上的点, 为
为 边的中点,
边的中点,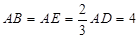 ,现将
,现将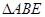 沿
沿 边折至
边折至 位置,且平面
位置,且平面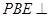 平面
平面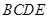 .
.  ;
;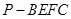 的体积.
的体积. 
 的底面为直角梯形,
的底面为直角梯形,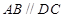 ,
,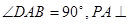 底面
底面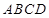 ,且
,且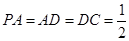 ,
,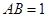 ,
,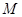 是
是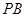 的中点。
的中点。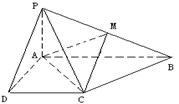
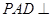 面
面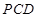 ;
;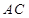 与
与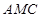 与面
与面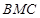 所成二面角的大小。
所成二面角的大小。 中,侧棱
中,侧棱 底面
底面 ,
,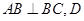 为
为 的中点,
的中点,  ,
, .
.
 平面
平面 ;
;  的体积.
的体积.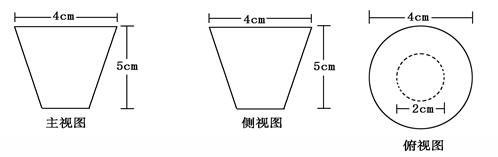
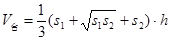
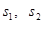 分别为上、下底面积
分别为上、下底面积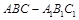 中,侧面
中,侧面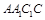 是边长为2的正方形,
是边长为2的正方形,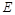 是
是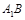 的中点,
的中点,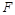 在棱
在棱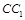 上.
上.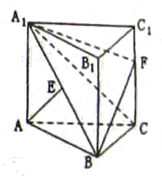
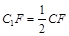 时,求三棱锥
时,求三棱锥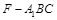 的体积.
的体积.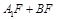 最小时,判断直线
最小时,判断直线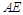 与
与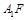 是否垂直,并证明结论.
是否垂直,并证明结论.