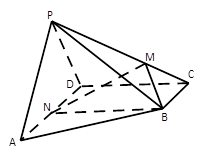
题目内容
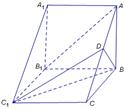
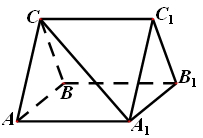
如图在三棱柱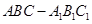 中,侧棱
中,侧棱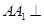 底面
底面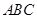 ,
,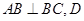 为
为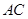 的中点,
的中点,  ,
, .
.
(1)求证: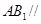 平面
平面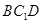 ;
;
(2)求四棱锥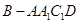 的体积.
的体积.
(1)证明如下 (2)3
解析试题分析:(1)证明:连接 ,设
,设 与
与 相交于点
相交于点 ,连接
,连接 ,
,
∵ 四边形 是平行四边形, ∴点
是平行四边形, ∴点 为
为 的中点.
的中点.
∵ 为
为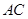 的中点,∴
的中点,∴ 为△
为△ 的中位线,
的中位线,
∴  . ∵
. ∵
 平面
平面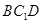 ,
, 平面
平面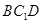 ,
,
∴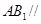 平面
平面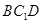 .
.
(2) ∵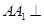 平面
平面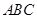 ,
, 平面
平面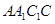 ,
,
∴ 平面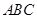
 平面
平面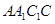 ,且平面
,且平面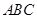
 平面
平面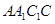
 .
.
作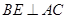 ,垂足为
,垂足为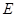 ,则
,则 平面
平面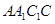 , ∵
, ∵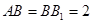 ,
, ,
,
在Rt△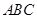 中,
中,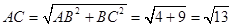 ,
, ,
,
∴四棱锥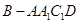 的体积
的体积

 .∴四棱锥
.∴四棱锥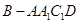 的体积为
的体积为 .
.
考点:直线与平面垂直的判定定理;直线与平面平行的判定定理;几何体的体积。
点评:在立体几何中,常考的定理是:直线与平面垂直的判定定理、直线与平面平行的判定定理。当然,此类题目也经常要我们求出几何体的体积和表面积。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
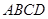 中
中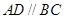 ,
, ,
,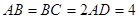 ,
, 、
、 分别是
分别是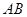 、
、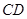 上的点,
上的点,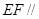
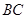 ,
,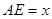 .沿
.沿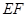 将梯形
将梯形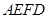 翻折,使平面
翻折,使平面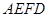 ⊥平面
⊥平面 (如图).
(如图).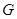 是
是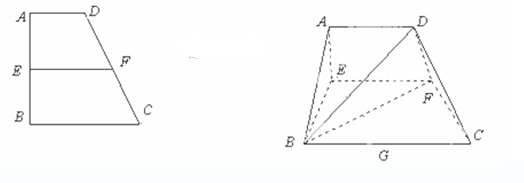
 时,求证:
时,求证: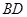 ⊥
⊥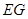 ;
; 变化时,求三棱锥
变化时,求三棱锥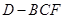 体积的最大值.
体积的最大值. 
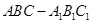 中,
中,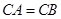 ,
,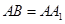 ,
,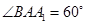 。
。
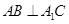 ;
;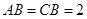 ,
,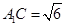 ,求三棱柱
,求三棱柱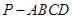 中,
中,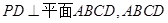 是正方形,E是
是正方形,E是 的中点,
的中点,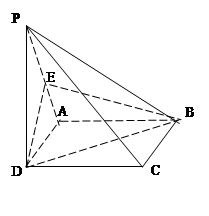
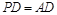 ,求 PC与面AC所成的角
,求 PC与面AC所成的角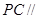 平面
平面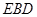
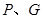 分别是
分别是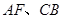 中点
中点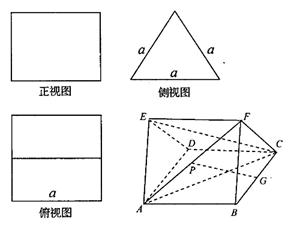
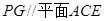 .
.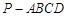 中
中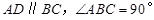 ,
,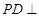 平面
平面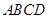 ,
,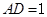 ,
,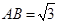 ,
,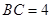 .
.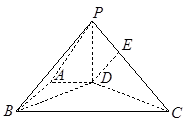
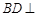
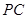 ;
;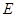 在棱
在棱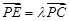 ,若
,若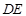 ∥平面
∥平面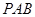 ,求
,求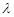 的值.
的值.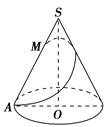
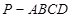 的侧面
的侧面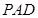 垂直于底面
垂直于底面 ,
,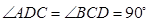
 ,
,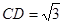 ,
,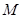 在棱
在棱 上,
上,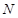 是
是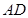 的中点,二面角
的中点,二面角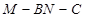 为
为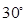 求
求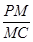 的值;
的值;