题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的定义域D,并判断
的定义域D,并判断![]() 的奇偶性;
的奇偶性;
(2)如果当![]() 时,
时,![]() 的值域是
的值域是![]() ,求a的值;
,求a的值;
(3)对任意的m,![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ,若存在,求出t,若不存在,请说明理由.
,若存在,求出t,若不存在,请说明理由.
【答案】(1)定义域为![]() ,奇函数;(2)
,奇函数;(2)![]() ;(3)存在,
;(3)存在,![]() ,详见解析
,详见解析
【解析】
(1)根据真数大于零可得到不等式求得定义域;由对数运算法则可证得![]() ,从而可知函数为奇函数;
,从而可知函数为奇函数;
(2)根据复合函数单调性可证得![]() 为定义域内的增函数,从而得到
为定义域内的增函数,从而得到![]() ,构造出关于
,构造出关于![]() 的方程,解方程求得
的方程,解方程求得![]() 的值;
的值;
(3)假设存在后,可根据对数运算法则得到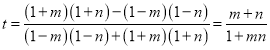 ;采用作差法验证出
;采用作差法验证出![]() ,从而可证得成立,并得到此时
,从而可证得成立,并得到此时![]() .
.
(1)由函数有意义可得:![]() ,解得:
,解得:![]()
![]() 的定义域为
的定义域为![]()
![]()
![]() 是
是![]() 上的奇函数
上的奇函数
(2)![]()
![]() 为
为![]() 上的减函数,
上的减函数,![]() 为
为![]() 上的减函数
上的减函数
![]() 在
在![]() 上单调递增
上单调递增 ![]() ,即
,即![]()
![]() ,解得:
,解得:![]() (舍)或
(舍)或![]()
![]()
(3) ,
,![]()
假设存在![]() ,使得
,使得![]() ,则:
,则:![]()
![]()
解得: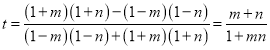
![]()
![]() ,
,![]()
![]()
![]()
又![]()
![]()
![]()
![]() 对任意的
对任意的![]() ,存在
,存在![]() 满足
满足![]() ,此时
,此时![]()

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
【题目】某电视台为宣传本市,随机对本市内![]() 岁的人群抽取了
岁的人群抽取了![]() 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |

(1)分别求出![]() 的值;
的值;
(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.