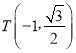题目内容
【题目】已知数列![]() 和
和![]() ,记
,记![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() 关于m的表达式;
关于m的表达式;
(3)若数列![]() 和
和![]() 均是项数为
均是项数为![]() 项的有穷数列.,现将
项的有穷数列.,现将![]() 和
和![]() 中的项一一取出,并按照从小到大的顺序排成一列,得到
中的项一一取出,并按照从小到大的顺序排成一列,得到![]() .求证:对于给定的
.求证:对于给定的![]() ,
,![]() 的所有可能取值的奇偶性相同.
的所有可能取值的奇偶性相同.
【答案】(1) ![]() ,
,![]() ;(2)
;(2) 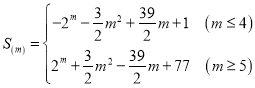 ;(3)证明详见解析.
;(3)证明详见解析.
【解析】
(1)将![]() 的值算出,代入即可;
的值算出,代入即可;
(2)遇绝对值要去绝对值,讨论![]() 的正负,分成两种情况去求
的正负,分成两种情况去求![]() 的表达式;
的表达式;
(3)因为交换![]() 和
和![]() 的值,
的值,![]() 的值不变,所以去绝对值等于
的值不变,所以去绝对值等于![]() 和
和![]() 中的大值减小值,不妨设
中的大值减小值,不妨设![]() 为
为![]() 和
和![]() 中的大值,
中的大值,![]() 为
为![]() 和
和![]() 中的小值,则
中的小值,则![]() ,而当m确定时,
,而当m确定时,![]() 为定值,即
为定值,即![]() 和
和![]() 的奇偶性相同.
的奇偶性相同.
(1)![]()
![]()
![]()
![]()
(2)若![]() ,求
,求![]() 关于m的表达式;
关于m的表达式;
①当![]() 时,
时,![]()
则当![]() 时,
时,
![]()
![]()
![]()
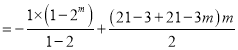
![]()
②当![]() 时,
时,![]()
则当![]() 时,
时,
![]()
![]()
![]()
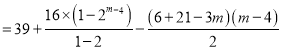
![]()

(3)设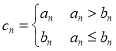 ,
,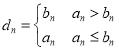 ,
,
则![]()
![]()
![]()
设![]() ,
,![]() ,
,
则![]()
![]()
![]() 恒为偶数,
恒为偶数,
![]() 与
与![]() 的奇偶性相同,
的奇偶性相同,
![]() 对于给定的
对于给定的![]() ,
,![]() 的奇偶性确定了,则
的奇偶性确定了,则![]() 的奇偶性也确定了.
的奇偶性也确定了.
即对于给定的![]() ,
,![]() 的所有可能取值的奇偶性相同.
的所有可能取值的奇偶性相同.

【题目】已知直线![]() .
.
(1)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,求
,求![]() 的面积的最小值并求此时直线
的面积的最小值并求此时直线![]() 的方程;
的方程;
(3)已知点![]() ,若点
,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值并求此时直线
的最大值并求此时直线![]() 的方程.
的方程.
【题目】近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000t生活垃圾.经分拣以后数据统计如下表(单位:![]() ):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
厨余垃圾”箱 | 可回收物”箱 | 其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
A.厨余垃圾投放正确的概率为![]()
B.居民生活垃圾投放错误的概率为![]()
C.该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱
D.厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差为20000