题目内容
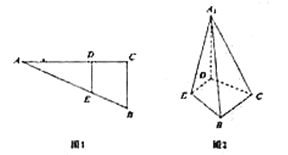
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 长为多少时,异面直线
长为多少时,异面直线![]() ,
,![]() 所成的角最小,并求出此时所成角的余弦值.
所成的角最小,并求出此时所成角的余弦值.
【答案】(Ⅰ)详见解析(Ⅱ)当![]() 时,异面直线
时,异面直线![]() ,
,![]() 所成的角最小,此时所成角的余弦值为
所成的角最小,此时所成角的余弦值为![]()
【解析】
(Ⅰ)根据线线垂直![]() 线面垂直(Ⅱ)利用垂直关系写出函数关系,求函数的最小值,最后结合余弦函数的单调性可求得。
线面垂直(Ⅱ)利用垂直关系写出函数关系,求函数的最小值,最后结合余弦函数的单调性可求得。
解:(Ⅰ)证明:因为 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
 平面
平面![]() ;
;
(Ⅱ)如图,连结![]() ,并设
,并设![]() ,
,![]() ,
,![]() ,
,
由(Ⅰ)中![]() 平面
平面![]() ,所以有
,所以有![]() ,从而在
,从而在![]() 中,
中,
![]() ,
,
又在![]() 中,
中,![]() ,
,
显然,当![]() 时,
时,![]() ,
,
即![]() (或是
(或是![]() 为
为![]() 中点)时,线段
中点)时,线段![]() 的长度有最小值,最小值是
的长度有最小值,最小值是![]() .
.
又因为![]() ,且
,且![]() ,则
,则![]() 即为异面直线
即为异面直线![]() ,
,![]() 所成的角,
所成的角,
又在![]() 中,
中, .结合余弦函数在锐角范围上是单调递减函数,所以当
.结合余弦函数在锐角范围上是单调递减函数,所以当![]() 取最大
取最大![]() 时,
时,![]() 取最小.
取最小.
综上,当![]() 时,异面直线
时,异面直线![]() ,
,![]() 所成的角最小,此时所成角的余弦值为
所成的角最小,此时所成角的余弦值为![]() .
.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目