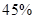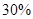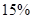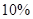题目内容
设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ＝0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ＝1.
(1)求概率P(ξ＝0)；
(2)求ξ的分布列，并求其数学期望E(ξ)．
(1)求概率P(ξ＝0)；
(2)求ξ的分布列，并求其数学期望E(ξ)．
(1)
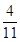(2) 随机变量ξ的分布列是
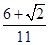
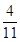(2) 随机变量ξ的分布列是| ξ | 0 | 1 |  |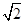
| P(ξ) | |  |  |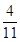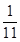
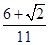
解 (1)若两条棱相交，则交点必为正方体8个顶点中的1个，过任意1个顶点恰有3条棱，所以共有8C32对相交棱，因此P(ξ＝0)＝
＝
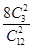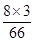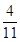＝.(2)若两条棱平行，则它们的距离为1或
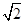，其中距离为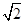的共有6对，故P(ξ＝)＝
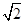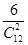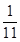＝，于是P(ξ＝1)＝1－P(ξ＝0)－P(ξ＝
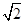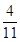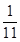)＝1－－＝，所以随机变量ξ的分布列是
| ξ | 0 | 1 | |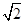
| P(ξ) | | | |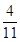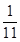
＋×＝.
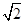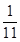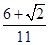练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
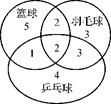
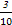
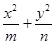＝1表示的曲线是焦点在x轴上的双曲线的概率为________．
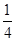，得到B公司面试的概率为p，且两个公司是否让其面试是独立的，记X为小王得到面试的公司个数．若X＝0时的概率P(X＝0)＝
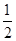，则随机变量X的数学期望为________．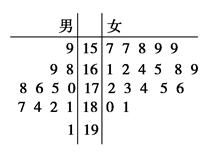
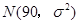，其中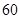
分以下的考生人数占
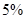，则数学成绩在
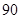至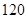
分之间的考生人数所占百分比约为 （ ）
