Question

【题目】如图，在平面四边形ABCD中，已知∠A= ，∠B= ，AB=6，在AB边上取点E，使得BE=1，连接EC，ED．若∠CED= ，EC= ．

（Ⅰ）求sin∠BCE的值；
（Ⅱ）求CD的长．

Answer 1

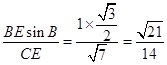【答案】解：（Ⅰ）在△CBE中，由正弦定理得 ，sin∠BCE= ， （Ⅱ）在△CBE中，由余弦定理得CE2=BE2+CB2﹣2BECBcos120°，即7=1+CB2+CB，解得CB=2．
由余弦定理得CB2=BE2+CE2﹣2BECEcos∠BECcos∠BEC= ．sin∠BEC= ，
sin∠AED=sin（1200+∠BEC）= ，cos∠AED= ，
在直角△ADE中，AE=5， ═cos∠AED= ，DE=2 ，
在△CED中，由余弦定理得CD2=CE2+DE2﹣2CEDEcos120°=49
∴CD=7．
【解析】（Ⅰ）在△CBE中，正弦定理求出sin∠BCE；（Ⅱ）在△CBE中，由余弦定理得CE2=BE2+CB2﹣2BECBcos120°，得CB．由余弦定理得CB2=BE2+CE2﹣2BECEcos∠BECcos∠BECsin∠BEC、cos∠AED在直角△ADE中，求得DE=2 ，在△CED中，由余弦定理得CD2=CE2+DE2﹣2CEDEcos120°即可