题目内容
18. 如图,矩形ABCD中,对角线AC、BD的交点为G,AD⊥平面ABE,AE⊥EB,AE=EB=BC=2,F为CE上的点,且BF⊥CE.
如图,矩形ABCD中,对角线AC、BD的交点为G,AD⊥平面ABE,AE⊥EB,AE=EB=BC=2,F为CE上的点,且BF⊥CE.(Ⅰ) 求证:AE⊥平面BCE;
(Ⅱ)求三棱锥C-GBF的体积.
分析 (Ⅰ)利用线面垂直的性质及判定可得BC⊥平面ABE,可得BC⊥AE.再利用线面垂直的判定定理可得AE⊥平面BCE;
(Ⅱ)由三角形的中位线定理可得:FG∥AE,$FG=\frac{1}{2}AE=1$.利用线面垂直的性质可得FG⊥平面BCE.再利用“等体积变形”即可得出VC-GBF=VG-BCF计算出即可.
解答 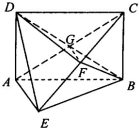 (I)证明:∵AD⊥面ABE,AD∥BC,
(I)证明:∵AD⊥面ABE,AD∥BC,
∴BC⊥面ABE,AE?平面ABE,
∴AE⊥BC.…(4分)
又∵AE⊥EB,且BC∩EB=B,∴AE⊥面BCE.…(5分)
(II)解:∵在△BCE中,EB=BC=2,BF⊥CE,
∴点F是EC的中点,且点G是AC的中点,…(7分)
∴FG∥AE且$FG=\frac{1}{2}AE=1$. …(8分)
∵AE⊥面BCE,∴FG⊥面BCE.
∴GF是三棱锥G-BFC的高 …(9分)
在Rt△BCE中,EB=BC=2,且F是EC的中点
${S_{△BCF}}=\frac{1}{2}{S_{△BCE}}=\frac{1}{2}•\frac{1}{2}BE•BC=1$.…(11分)
∴${V_{C-BFG}}={V_{G-BCF}}=\frac{1}{3}{S_{△BCF}}•FG=\frac{1}{3}$.…(12分)
点评 本题中考查了线面垂直的判定定理和性质定理、三角形的中位线定理、三棱锥的体积计算公式及“等体积变形”等基础知识和基本技能,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
9.若$|{\overrightarrow a}|=2$,$|{\overrightarrow b}|=1$,$\overrightarrow a$与$\overrightarrow b$的夹角为60°,则$\overrightarrow a•\overrightarrow b$=( )
| A. | 2 | B. | 1 | C. | 2$\sqrt{2}$ | D. | 4 |
10. 某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
(1)在给定的坐标系中画出表中数据的散点图;
(2)试根据最小二乘法原理,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并在给定的坐标系中画出回归直线;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的学生的判断力.
参考公式:用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}},\hat a=\overline y-\hat b\overline x$.
 某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)试根据最小二乘法原理,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并在给定的坐标系中画出回归直线;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的学生的判断力.
参考公式:用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}},\hat a=\overline y-\hat b\overline x$.
7.当a>1时,函数y=a-x与y=logax的图象是( )
| A. |  | B. |  | C. |  | D. |  |