题目内容
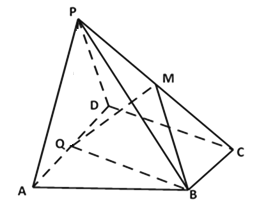
【题目】在四棱柱![]() 中,底面
中,底面![]() 为矩形,面
为矩形,面![]() ⊥平面
⊥平面![]() ,
,![]() =
=![]() =
=![]() =
=![]() ,
,![]() =2,
=2,![]() 是
是![]() 的中点.
的中点.
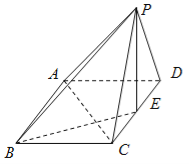
(Ⅰ)求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)求BD与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】(Ⅰ)∵PD=PC,E为CD的中点,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD,
∴PE⊥AC,(2分)
在Rt△BCE和Rt△ABC中,![]() ,∠ABC=∠BCE=90°,
,∠ABC=∠BCE=90°,
∴Rt△BCE∽Rt△ABC,(4分)
∴∠BAC=∠CBE,∠ACB=∠BEC,
∴∠EBC+∠ACB=∠CAB+∠ACB=90°,
∴BE⊥CA,(5分)
∵BE∩PE=E,
∴AC⊥平面PBE,
∴AC⊥PB;(6分)
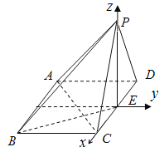
(Ⅱ)以E为坐标原点,如图建立空间直角坐标系,则P(0,0,1),C(1,0,0),![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,(8分)
,(8分)
设平面![]() 的法向量为
的法向量为![]() ,则
,则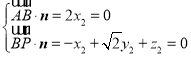 ,取
,取![]() =
=![]() ,则
,则![]() =0,
=0,![]() =-2,∴
=-2,∴![]() =(0,
=(0,![]() ,-2),(10分)
,-2),(10分)
设BD与平面![]() 所成角为
所成角为![]() ,
,
则![]() =
=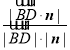 =
=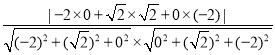 =
=![]() ,(11分)
,(11分)
∴BD与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .(12分)
.(12分)

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】现阶段全国多地空气质量指数“爆表”.为探究车流量与![]() 浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到
浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到![]() 月某天
月某天![]() 个不同时段车流量与
个不同时段车流量与![]() 浓度的数据,如下表:
浓度的数据,如下表:
车流量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据上表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)规定当![]() 浓度平均值在
浓度平均值在![]() ,空气质量等级为优;当
,空气质量等级为优;当![]() 浓度平均值在
浓度平均值在![]() ,空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
,空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程: ![]() ,其中
,其中 ,
, ![]() .
.
【题目】某中学调查了某班全部50名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 6 |
未参加演讲社团 | 6 | 30 |
(I)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(II)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3,现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.