题目内容
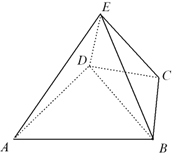
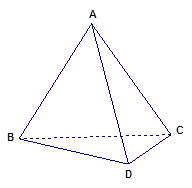
如图,几何体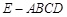 是四棱锥,△
是四棱锥,△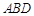 为正三角形,
为正三角形,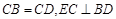 .
.
(1)求证: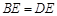 ;
;
(2)若∠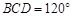 ,M为线段AE的中点,求证:
,M为线段AE的中点,求证: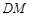 ∥平面
∥平面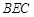 .
.
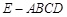 是四棱锥,△
是四棱锥,△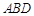 为正三角形,
为正三角形,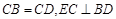 .
.(1)求证:
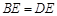 ;
;(2)若∠
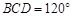 ,M为线段AE的中点,求证:
,M为线段AE的中点,求证: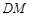 ∥平面
∥平面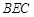 .
.
(1)见解析 (2) 见解析
本题考查直线与平面平行的判定,考查线面垂直的判定定理与面面平行的判定定理的应用,着重考查分析推理能力与表达、运算能力,属于中档题.
(1)设BD中点为O,连接OC,OE,则CO⊥BD,CE⊥BD,于是BD⊥平面OCE,从而BD⊥OE,即OE是BD的垂直平分线,问题解决;
(2)证法一:取AB中点N,连接MN,DN,MN,易证MN∥平面BEC,DN∥平面BEC,由面面平行的判定定理即可证得平面DMN∥平面BEC,又DM?平面DMN,于是DM∥平面BEC;
证法二:延长AD,BC交于点F,连接EF,易证AB=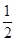 AF,D为线段AF的中点,连接DM,则DM∥EF,由线面平行的判定定理即可证得结论.
AF,D为线段AF的中点,连接DM,则DM∥EF,由线面平行的判定定理即可证得结论.
(I)设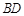 中点为O,连接OC,OE,则由
中点为O,连接OC,OE,则由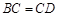 知,
知,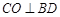 ,…………2分
,…………2分
又已知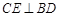 ,所以
,所以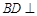 平面OCE. …………4分
平面OCE. …………4分
所以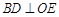 ,即OE是BD的垂直平分线,
,即OE是BD的垂直平分线,
所以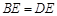 .…………6分
.…………6分
(II)取AB中点N,连接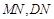 ,
,
∵M是AE的中点,∴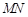 ∥
∥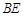 ,…………8分
,…………8分
∵△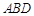 是等边三角形,∴
是等边三角形,∴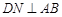 .
.
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即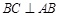 ,
,
所以ND∥BC,…………10分
所以平面MND∥平面BEC,故DM∥平面BEC. …………12分
(1)设BD中点为O,连接OC,OE,则CO⊥BD,CE⊥BD,于是BD⊥平面OCE,从而BD⊥OE,即OE是BD的垂直平分线,问题解决;
(2)证法一:取AB中点N,连接MN,DN,MN,易证MN∥平面BEC,DN∥平面BEC,由面面平行的判定定理即可证得平面DMN∥平面BEC,又DM?平面DMN,于是DM∥平面BEC;
证法二:延长AD,BC交于点F,连接EF,易证AB=
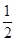 AF,D为线段AF的中点,连接DM,则DM∥EF,由线面平行的判定定理即可证得结论.
AF,D为线段AF的中点,连接DM,则DM∥EF,由线面平行的判定定理即可证得结论.(I)设
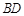 中点为O,连接OC,OE,则由
中点为O,连接OC,OE,则由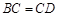 知,
知,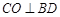 ,…………2分
,…………2分又已知
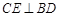 ,所以
,所以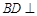 平面OCE. …………4分
平面OCE. …………4分所以
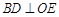 ,即OE是BD的垂直平分线,
,即OE是BD的垂直平分线,所以
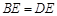 .…………6分
.…………6分(II)取AB中点N,连接
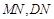 ,
,∵M是AE的中点,∴
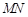 ∥
∥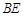 ,…………8分
,…………8分∵△
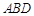 是等边三角形,∴
是等边三角形,∴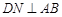 .
.由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即
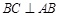 ,
,所以ND∥BC,…………10分
所以平面MND∥平面BEC,故DM∥平面BEC. …………12分

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 中,
中,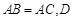 为
为 的中点,
的中点,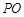 平面
平面 ,垂足
,垂足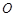 落在线段
落在线段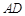 上,已知
上,已知
 ;
;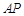 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 为直二面角?若存在,求出
为直二面角?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 
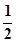 AD=1,CD=
AD=1,CD=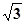 .
.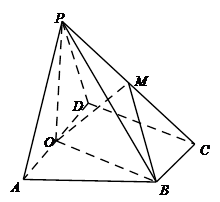
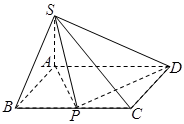
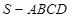 的底面是矩形,
的底面是矩形,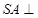 底面
底面 ,
,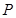 为
为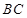 边的中点,
边的中点,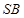 与平面
与平面 所成的角为
所成的角为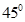 ,且
,且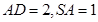 。
。
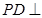 平面
平面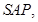
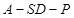 的大小的正切值.
的大小的正切值.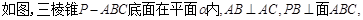
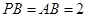 ,
,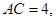
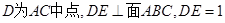 ,P、E在
,P、E在 同侧,连接PE、AE.
同侧,连接PE、AE.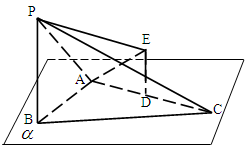
 求证:BC//面APE;
求证:BC//面APE; 设F是
设F是 ,求直线EF与面APF所成角的大小
,求直线EF与面APF所成角的大小 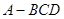 中,面
中,面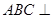 面
面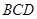 ,
,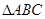 是正三角形,
是正三角形,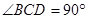 .
.
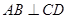 ;
;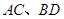 所成角的余弦值为
所成角的余弦值为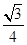 ,求二面角
,求二面角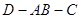 的大小;
的大小;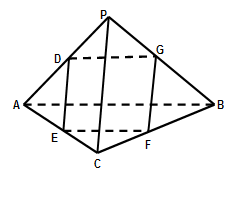
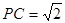 ,求四面体PABC的体积.
,求四面体PABC的体积.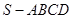 的底面边长为
的底面边长为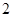 ,高为
,高为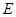 是边
是边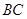 的中点,动点
的中点,动点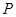 在这个棱锥表面上运动,并且总保持
在这个棱锥表面上运动,并且总保持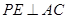 ,则动点
,则动点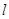 、
、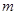 与平面
与平面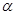 、
、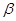 的命题中,正确的是 ( )
的命题中,正确的是 ( )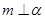 ,
,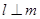 ,则
,则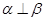 ,
,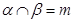 ,
,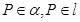 ,且
,且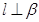
 ,
,