题目内容
(本小题满分12分)
在三棱柱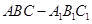 中,侧棱
中,侧棱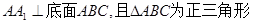 ,点
,点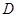 是
是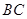 的中点,
的中点,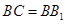 .
.
(1)求证: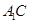 ∥平面
∥平面 ;
;
(2)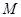 为棱
为棱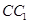 的中点,试证明:
的中点,试证明: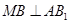 .
.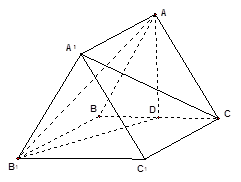
在三棱柱
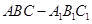 中,侧棱
中,侧棱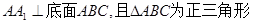 ,点
,点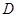 是
是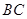 的中点,
的中点,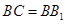 .
.(1)求证:
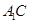 ∥平面
∥平面 ;
;(2)
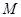 为棱
为棱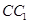 的中点,试证明:
的中点,试证明: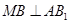 .
.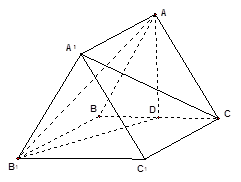
见解析。
本试题主要是考查了空间立体几何中线面平行和线线垂直的证明。
(1)连接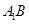 ,交
,交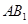 于点
于点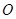 , 连接
, 连接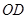 .
.
∵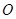 、
、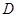 分别是
分别是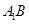 、
、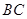 的中点,∴
的中点,∴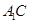 ∥
∥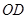 .
.
∵ 平面
平面 ,
,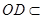 平面
平面 ,∴
,∴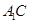 ∥平面
∥平面 .
.
(2)正三棱柱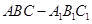 中,
中,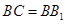 ,∴四边形
,∴四边形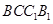 是正方形.
是正方形.
∵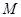 为
为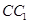 的中点,
的中点,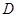 是
是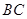 的中点,∴
的中点,∴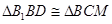 可得到
可得到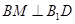 ,同时还有
,同时还有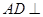
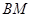 .,利用线面垂直的性质定理得到结论。
.,利用线面垂直的性质定理得到结论。
(1)证明:连接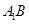 ,交
,交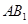 于点
于点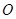 , 连接
, 连接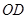 .
.
∵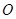 、
、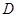 分别是
分别是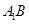 、
、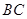 的中点,∴
的中点,∴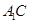 ∥
∥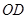 .
.
∵ 平面
平面 ,
,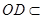 平面
平面 ,∴
,∴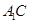 ∥平面
∥平面 .
.
(2)∵在正三棱柱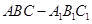 中,
中,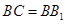 ,∴四边形
,∴四边形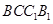 是正方形.
是正方形.
∵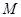 为
为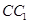 的中点,
的中点,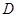 是
是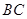 的中点,∴
的中点,∴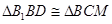 ,
,
∴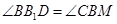 ,
,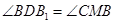 .
.
又∵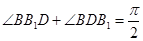 ,
, 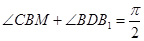 ,∴
,∴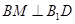 .
.
∵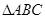 是正三角形,
是正三角形,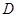 是
是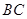 的中点,∴
的中点,∴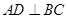 .
.
∵平面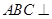 平面
平面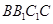 , 平面
, 平面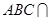 平面
平面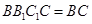 ,
,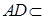 平面
平面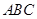 ,
,
∴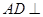 平面
平面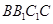 .
.
∵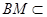 平面
平面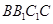 ,∴
,∴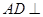
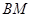 .
.
∵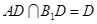 ,∴
,∴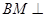 平面
平面 .
.
∵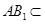 平面
平面 ,∴
,∴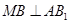 .
.
(1)连接
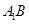 ,交
,交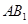 于点
于点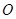 , 连接
, 连接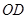 .
.∵
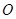 、
、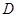 分别是
分别是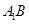 、
、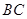 的中点,∴
的中点,∴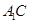 ∥
∥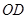 .
.∵
 平面
平面 ,
,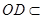 平面
平面 ,∴
,∴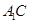 ∥平面
∥平面 .
.(2)正三棱柱
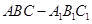 中,
中,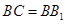 ,∴四边形
,∴四边形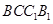 是正方形.
是正方形.∵
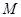 为
为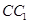 的中点,
的中点,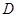 是
是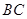 的中点,∴
的中点,∴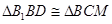 可得到
可得到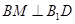 ,同时还有
,同时还有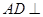
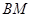 .,利用线面垂直的性质定理得到结论。
.,利用线面垂直的性质定理得到结论。(1)证明:连接
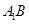 ,交
,交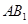 于点
于点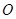 , 连接
, 连接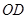 .
.∵
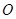 、
、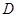 分别是
分别是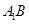 、
、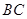 的中点,∴
的中点,∴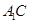 ∥
∥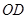 .
.∵
 平面
平面 ,
,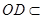 平面
平面 ,∴
,∴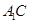 ∥平面
∥平面 .
. (2)∵在正三棱柱
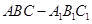 中,
中,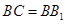 ,∴四边形
,∴四边形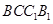 是正方形.
是正方形.∵
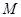 为
为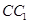 的中点,
的中点,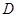 是
是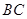 的中点,∴
的中点,∴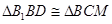 ,
,∴
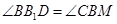 ,
,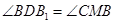 .
.又∵
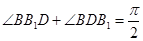 ,
, 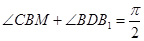 ,∴
,∴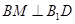 .
. ∵
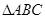 是正三角形,
是正三角形,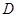 是
是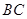 的中点,∴
的中点,∴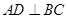 .
.∵平面
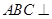 平面
平面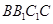 , 平面
, 平面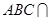 平面
平面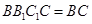 ,
,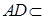 平面
平面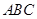 ,
,∴
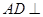 平面
平面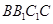 .
.∵
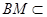 平面
平面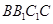 ,∴
,∴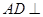
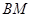 .
.∵
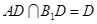 ,∴
,∴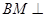 平面
平面 .
.∵
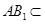 平面
平面 ,∴
,∴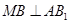 .
.
练习册系列答案
相关题目

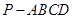 的底面是正方形,
的底面是正方形,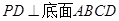 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=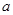 ,
,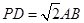
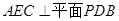 ;
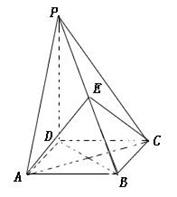
; 
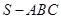 中,侧面
中,侧面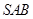 与侧面
与侧面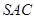 均为等边三角形,
均为等边三角形,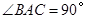 ,
,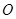 为
为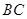 中点.
中点.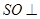 平面
平面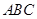 ;
;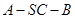 的余弦值.
的余弦值.
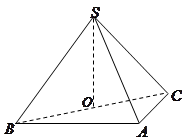
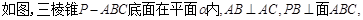
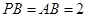 ,
,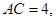
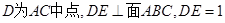 ,P、E在
,P、E在 同侧,连接PE、AE.
同侧,连接PE、AE.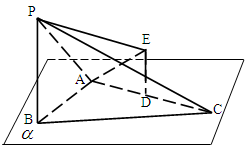
 求证:BC//面APE;
求证:BC//面APE; 设F是
设F是 ,求直线EF与面APF所成角的大小
,求直线EF与面APF所成角的大小 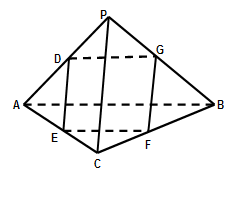
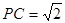 ,求四面体PABC的体积.
,求四面体PABC的体积. ,
,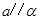 ,
,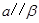 ,则
,则 与
与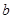 的位置关系是_______.
的位置关系是_______.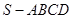 的底面边长为
的底面边长为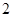 ,高为
,高为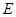 是边
是边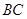 的中点,动点
的中点,动点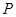 在这个棱锥表面上运动,并且总保持
在这个棱锥表面上运动,并且总保持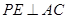 ,则动点
,则动点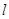 、
、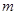 与平面
与平面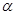 、
、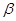 的命题中,正确的是 ( )
的命题中,正确的是 ( )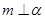 ,
,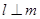 ,则
,则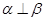 ,
,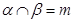 ,
,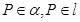 ,且
,且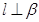
 ,
,