题目内容
【题目】已知数列![]() 满足:
满足:![]() (常数
(常数![]() ),
),![]() (
(![]() ,
,![]() ).数列
).数列![]() 满足:
满足:![]() (
(![]() ).
).
(1)求![]() ,
,![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在k,使得数列![]() 的每一项均为整数?若存在,求出k的所有可能值;若不存在,请说明理由.
的每一项均为整数?若存在,求出k的所有可能值;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2) ;(3)
;(3)![]()
【解析】
(1)经过计算可知:![]() ,由数列
,由数列![]() 满足:
满足:![]() ,从而可求
,从而可求![]() ,
,![]() ;
;
(2)由条件可知:![]() ,得
,得![]() ,两式相减整理得
,两式相减整理得![]() ,从而可求数列
,从而可求数列![]() 的通项公式;
的通项公式;
(3)假设存在正数![]() ,使得数列
,使得数列![]() 的每一项均为整数则由(2)可知
的每一项均为整数则由(2)可知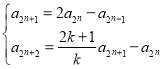 ,由
,由![]() ,
,![]() ,可求得
,可求得![]() ,2,证明
,2,证明![]() ,2时,满足题意,说明
,2时,满足题意,说明![]() 为1,2时,数列
为1,2时,数列![]() 是整数列即可.
是整数列即可.
(1)由已知得,![]() ,
,
所以![]() ,
,![]() .
.
(2)由条件可知:![]() (
(![]() ),①
),①
所以![]() (
(![]() ).②
).②
①![]() ②得
②得![]() .
.
即:![]() .
.
因此:![]() ,
,
故![]() (
(![]() ),又因为
),又因为![]() ,
,![]() ,
,
所以 .
.
(3)假设存在k,使得数列![]() 的每一项均为整数,则k为正整数.
的每一项均为整数,则k为正整数.
由(2)知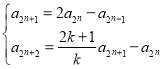 (
(![]() ,2,3…)③
,2,3…)③
由![]() ,
,![]() ,所以
,所以![]() 或2,
或2,
检验:当![]() 时,
时,![]() 为整数,
为整数,
利用![]() ,
,![]() ,
,![]() 结合③,
结合③,![]() 各项均为整数;
各项均为整数;
当![]() 时③变成
时③变成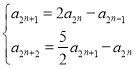 (
(![]() ,2,3…)
,2,3…)
消去![]() ,
,![]() 得:
得:![]() (
(![]() )
)
由![]() ,
,![]() ,所以偶数项均为整数,
,所以偶数项均为整数,
而![]() ,所以
,所以![]() 为偶数,故
为偶数,故![]() ,故数列
,故数列![]() 是整数列.
是整数列.
综上所述,k的取值集合是![]() .
.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()