题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程及
的极坐标方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 与曲线
与曲线![]() 、
、![]() 分别交于异于原点的点
分别交于异于原点的点![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 为参数),利用平方关系消去
为参数),利用平方关系消去![]() ,可得曲线的普通方程,把
,可得曲线的普通方程,把![]() ,
,![]() 代入可得曲线
代入可得曲线![]() 的极坐标方程;把曲线
的极坐标方程;把曲线![]() 的极坐标方程变形,代入
的极坐标方程变形,代入![]() ,
,![]() ,得曲线
,得曲线![]() 的直角坐标方程;(2)设
的直角坐标方程;(2)设![]() ,
,![]() ,
,![]() ,
,![]() ,把
,把![]() 用含有
用含有![]() 的三角函数表示,再利用基本不等式求最值.
的三角函数表示,再利用基本不等式求最值.
(1)由![]() 为参数),得曲线
为参数),得曲线![]() 的普通方程为
的普通方程为![]() ,
,
即![]()
由![]() ,
,![]() ,得曲线
,得曲线![]() 的极坐标方程为
的极坐标方程为![]() ;
;
![]() 曲线
曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() ,
,
由![]() ,
,![]() ,得曲线
,得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(2)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() .
.
当且仅当![]() 时等号成立,
时等号成立,
所以![]() 的最小值为
的最小值为![]() .
.

【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重;当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重;当![]() 数值小于20.5时,我们说体重较轻;身高大于或等于170
数值小于20.5时,我们说体重较轻;身高大于或等于170![]() 的我们说身高较高;身高小于170
的我们说身高较高;身高小于170![]() 的我们说身高较矮.
的我们说身高较矮.
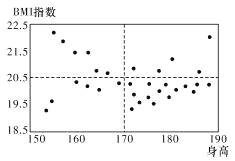
(1)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图所示,请根据所得信息,完成下列列联表,并判断是否有95%的把握认为男体育特长生的身高对
指数的数据如散点图所示,请根据所得信息,完成下列列联表,并判断是否有95%的把握认为男体育特长生的身高对![]() 指数有影响;
指数有影响;
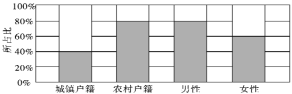
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(2)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献率
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献率![]() (保留两位有效数字);
(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 | -1.5 | -0.5 |
②通过残差分析,对于残差(绝对值)最大的那组数据,需要确认在样本点的采集中是否有人为的错误.已知通过重新采集发现,该组数据的体重应该为58(kg).请重新根据最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
(参考公式)
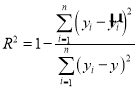 ,
,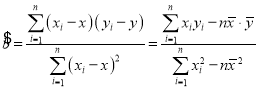 ,
,
![]() ,
,![]() ,
,
 (
(![]() ).
).
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(参考数据)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.