题目内容
2.A,B,C是球面上的三点,且AB=1,BC=2,∠ABC=120°,且球心到平面ABC的距离为3,则球的表面积为$\frac{220}{3}$π.分析 求出△ABC的外接圆的半径,利用球心到平面ABC的距离为3,可求出球的半径,然后求球的表面积.
解答 解:由题意AB=1,BC=2,∠ABC=120°,
可知AC=$\sqrt{1+4-2×1×2×(-\frac{1}{2})}$=$\sqrt{7}$,
设△ABC的外接圆的半径为r,则2r=$\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{21}}{3}$,
∴r=$\frac{\sqrt{21}}{3}$,
∵球心到平面ABC的距离为3,
正好是球心到BC的中点的距离,
∴球的半径是:R=$\sqrt{9+\frac{28}{3}}$=$\sqrt{\frac{55}{3}}$,
球的表面积是:4πR2=$\frac{220}{3}$π.
故答案为:$\frac{220}{3}$π.
点评 本题考查球的内接体问题,考查学生空间想象能力,是中档题.确定三角形ABC的形状以及利用球半径与球心O到平面ABC的距离的关系,是解好本题的前提.

练习册系列答案
相关题目
17.若一个几何体的三视图如图所示,则该几何体的体积为( )
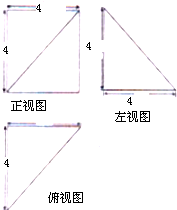

| A. | 64 | B. | $\frac{64}{3}$ | C. | 27 | D. | 36 |
7.已知a,b,c∈R,且a>b,ab≠0,则下列不等式一定成立的是( )
| A. | a3>b3 | B. | ac2>bc2 | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | a2>b2 |