题目内容
5.设数列{an}的前n项和为Sn,且${S_n}={n^2}+2n$,(Ⅰ)求数列{an}的通项公式;
(Ⅱ)用定义证明{an}是等差数列.
分析 (Ⅰ)根据n≥2时,an=Sn-Sn-1的关系即可求数列{an}的通项公式;
(Ⅱ)根据等差数列的定义进行证明即可.
解答 解:(Ⅰ)∵${S_n}={n^2}+2n$,
当n≥2时,an=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1;
∵a1=S1=3满足an=2n+1,
∴an=2n+1;
(Ⅱ)∵an=2n+1,
∴an+1-an=2(n+1)+1-(2n+1)=2,
∴{an}是首项为3,公差为2的等差数列.
点评 本题主要考查数列通项公式的求解以及等差数列的证明,利用n≥2时,an=Sn-Sn-1的关系是解决本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
16.若m>1,a=$\sqrt{m}$-$\sqrt{m-1}$,b=$\sqrt{m+1}$-$\sqrt{m}$,则以下结论正确的是( )
| A. | a>b | B. | a<b | C. | a=b | D. | a,b大小不定 |
20.根据如图框图,当输出的y=10时,输入的x为( )
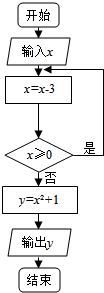

| A. | 4 | B. | 6或0 | C. | 0 | D. | 4或6 |
15.已知f(x)=$\left\{\begin{array}{l}{(3-a)x-1(x<1)}\\{lo{g}_{a}x(x≥1)}\end{array}\right.$是(-∞,+∞)上的增函数,那么a的取值范围是( )
| A. | (1,+∞) | B. | (-∞,3) | C. | [2,3) | D. | (1,3) |
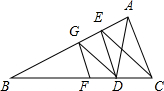 已知:△ABC中,E、G、D、F分别是边AB、CB上的一点,且GF∥ED∥AC,EF∥AD.
已知:△ABC中,E、G、D、F分别是边AB、CB上的一点,且GF∥ED∥AC,EF∥AD.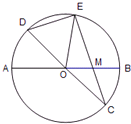 如图,已知在半径为4的⊙O中,AB,CD是⊙O的两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=$\sqrt{15}$.
如图,已知在半径为4的⊙O中,AB,CD是⊙O的两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=$\sqrt{15}$.