题目内容
设 是函数
是函数
 的零点.
的零点.
(1)证明: ;
;
(2)证明:
 .
.
 是函数
是函数
 的零点.
的零点.(1)证明:
 ;
;(2)证明:

 .
.(1)详见解析;(2)详见解析.
试题分析:(1)借助导数证明函数
 在
在 是单调函数,进而确定函数
是单调函数,进而确定函数 在
在 上有且只有一个零点,进而证明
上有且只有一个零点,进而证明 ;(2)先将原不等式化为两个不等式
;(2)先将原不等式化为两个不等式 与
与 ,先证明不等式
,先证明不等式 ,方法1先证明不等式
,方法1先证明不等式 ,然后利用放缩法证明
,然后利用放缩法证明 ,从而证明不等式
,从而证明不等式 成立,方法2是在不等式
成立,方法2是在不等式 的基础上利用数学归纳法直接证明不等式
的基础上利用数学归纳法直接证明不等式 成立;再证明不等式
成立;再证明不等式
先考察函数
 的单调性证明
的单调性证明 ,然后就
,然后就 时,将对
时,将对 进行放缩,
进行放缩, ,进而证明
,进而证明 。
。试题解析:(1)因为
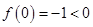 ,
, ,且
,且 在
在 上的图像是一条连续曲线,
上的图像是一条连续曲线,所以函数
 在
在 内有零点. 1分
内有零点. 1分因为
 ,
,所以函数
 在
在 上单调递增. 2分
上单调递增. 2分所以函数
 在
在 上只有一个零点,且零点在区间
上只有一个零点,且零点在区间 内.
内.而
 是函数
是函数 的零点,
的零点,所以
 . 3分
. 3分(2)先证明左边的不等式:
因为
 ,
,由(1)知
 ,
,所以
 . 4分
. 4分即
 .
.所以
 . 5分
. 5分所以
 . 6分
. 6分以下证明
 . ①
. ①方法1(放缩法):因为
 , 7分
, 7分所以
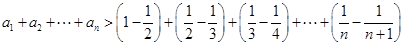
 . 9分
. 9分方法2(数学归纳法):1)当
 时,
时, ,不等式①成立.
,不等式①成立.2)假设当
 (
( )时不等式①成立,即
)时不等式①成立,即 .
.那么

 .
.以下证明
 . ②
. ②即证
 .
.即证
 .
.由于上式显然成立,所以不等式②成立.
即当
 时不等式①也成立.
时不等式①也成立.根据1)和2),可知不等式①对任何
 都成立.
都成立.所以
 . 9分
. 9分再证明右边的不等式:
当
 时,
时, .
.由于
 ,
, ,
,所以
 . 10分
. 10分由(1)知
 ,且
,且 ,所以
,所以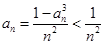 . 11分
. 11分因为当
 时,
时, , 12分
, 12分所以当
 时,
时,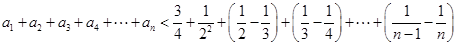
 .
.所以当
 时,都有
时,都有 .
.综上所述,

 . 14分
. 14分
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 +
+ +…+
+…+ ,计算得f(2)=
,计算得f(2)= ,f(4)>2,
,f(4)>2, f(16)>3,观察上述结果,可推测一般的结论为 .
f(16)>3,观察上述结果,可推测一般的结论为 .  ,求出
,求出 猜想出数列的前n项和Sn的表达式
猜想出数列的前n项和Sn的表达式 的面积
的面积 ,猜想出椭圆
,猜想出椭圆 的面积
的面积
 ,
,  ,
,  ,
, ,
, 按上述规律展开后,发现等式右边含有“
按上述规律展开后,发现等式右边含有“ ”这个数,则
”这个数,则 _______.
_______. ,把
,把 表示
表示 ,当
,当 时,
时, ;当
;当 时,
时, 为0或1. 记
为0或1. 记 为上述表示中
为上述表示中 ,
, ,
, ,
, ),若
),若 ,
, ,
, ,则(1)
,则(1) .
. .
. 是无理数,所以
是无理数,所以 中,
中, ,过
,过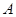 作
作 边的高
边的高 ,有下列结论
,有下列结论 。请利用上述结论,类似地推出在空间四面体
。请利用上述结论,类似地推出在空间四面体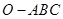 中,若
中,若
 ,
, 点到平面
点到平面 ,则 .
,则 . …,若
…,若 (a,t均为正实数),则类比以上等式,可推测a,t的值,a+t= .
(a,t均为正实数),则类比以上等式,可推测a,t的值,a+t= .