题目内容
7.(1)f(x)=|logax|,(0<a<1)减区间为(0,1].(2)直线y=2a与y=|ax-1|,a>0的图象有两个公共点,则a范围(0,$\frac{1}{2}$).
分析 (1)由题意画出图形,由图形可得函数的减区间;
(2)对a分类作出y=2a与y=|ax-1|的图象,数形结合得答案.
解答 解:(1)作出函数f(x)=|logax|,(0<a<1)的图象如图,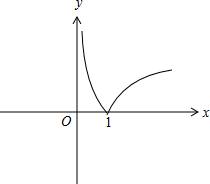
由图可知,f(x)=|logax|,(0<a<1)减区间为(0,1];
(2)当a>1时,作出y=2a与y=|ax-1|的图象如图,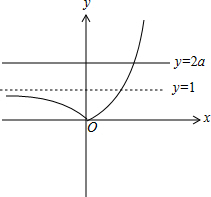
由图可知,直线y=2a与y=|ax-1|,a>1的图象只有一个公共点;
当0<a<1时,作出y=2a与y=|ax-1|的图象如图,
由图可知,要使直线y=2a与y=|ax-1|,0<a<1的图象有两个公共点,
则a的范围是(0,$\frac{1}{2}$).
故答案为:(1)(0,1];(2)(0,$\frac{1}{2}$).
点评 本题考查复合函数的单调性,考查了函数零点的判定方法,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
19.设P={x|x2-6x-16<0},Q={x|x(x-1)>6},则P∩Q=( )
| A. | {x|x>-2} | B. | {x|-2<x<8} | C. | {x|3<x<8} | D. | {x|-2<x<3] |
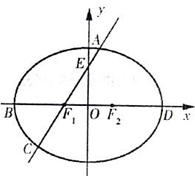 如图,在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1(a>0)中,F1、F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆位于第一象限内的部分上的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD.
如图,在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1(a>0)中,F1、F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆位于第一象限内的部分上的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD.