题目内容
9.已知双曲线$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=1$的焦点为F1,F2,双曲线与椭圆$\frac{{x}^{2}}{29}+\frac{{y}^{2}}{4}=1$交于点P,则|PF1|•|PF2|的值为13.分析 由题意可得双曲线和椭圆具有相同的焦点,不妨设交点P在第一象限,分别运用双曲线和椭圆的定义,即可得到结论.
解答 解:由题意可得双曲线和椭圆具有相同的焦点,
不妨设交点P在第一象限,
由双曲线的定义可得|PF1|-|PF2|=2×4=8,①
由椭圆的定义可得|PF1|+|PF2|=2$\sqrt{29}$,②
②2-①2,可得|PF1|•|PF2|=13.
故答案为:13.
点评 本题考查椭圆和双曲线的定义、方程和性质,注意运用定义法解题,考查运算能力,属于中档题.

练习册系列答案
相关题目
19.设复数z1=1-i,z2=-1+xi(x∈R),若z1z2为纯虚数,则x的值是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
4.双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=-1的焦点坐标为( )
| A. | (±3,0) | B. | (±5,0) | C. | (0,±5) | D. | (0,±$\sqrt{7}$) |
1.函数y=$\sqrt{{(15+2x{-x}^{2})}^{3}}$的定义域是( )
| A. | {x|-3≤x≤5} | B. | {x|-3<x<5} | C. | {x|x≥5或x≤-3} | D. | R |
19.设P={x|x2-6x-16<0},Q={x|x(x-1)>6},则P∩Q=( )
| A. | {x|x>-2} | B. | {x|-2<x<8} | C. | {x|3<x<8} | D. | {x|-2<x<3] |
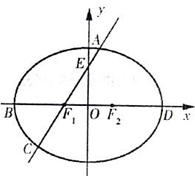 如图,在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1(a>0)中,F1、F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆位于第一象限内的部分上的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD.
如图,在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1(a>0)中,F1、F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆位于第一象限内的部分上的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD.