题目内容
已知函数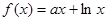 ,其中
,其中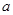 为常数,设
为常数,设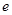 为自然对数的底数.
为自然对数的底数.
(1)若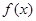 在区间
在区间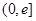 上的最大值为-3,求
上的最大值为-3,求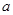 的值;
的值;
(2)当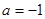 时,试推断方程
时,试推断方程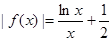 是否有实数解.
是否有实数解.
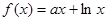 ,其中
,其中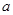 为常数,设
为常数,设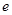 为自然对数的底数.
为自然对数的底数.(1)若
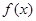 在区间
在区间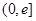 上的最大值为-3,求
上的最大值为-3,求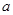 的值;
的值;(2)当
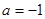 时,试推断方程
时,试推断方程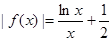 是否有实数解.
是否有实数解.(1)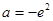 ;(2)见解析.
;(2)见解析.
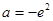 ;(2)见解析.
;(2)见解析.第一问中利用导数的思想求解极值,然后利用端点值和极值比较大小,得到最值。
第二问中,利用由(1)知当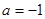 时,
时, ,所以
,所以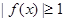
又令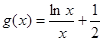 ,
,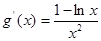 ,令
,令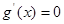 ,得
,得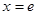
当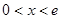 时,
时,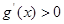 ,
,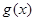 在
在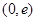 上单调递增;
上单调递增;
当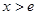 时,
时,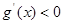 ,
,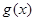 在
在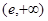 上单调递减;
上单调递减;
∴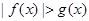 ,即
,即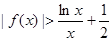
因此得到结论。
解:(1)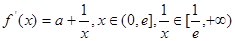 ………1分
………1分
①若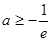 ,则
,则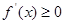 ,从而
,从而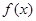 在
在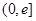 上是增函数,
上是增函数,
∴ ,不合题意………2分
,不合题意………2分
②若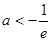 ,则由
,则由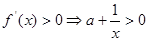 ,即
,即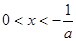 ,
,
由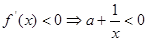 ,即
,即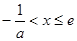
从而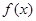 在
在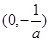 上是增函数,在
上是增函数,在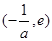 为减函数
为减函数
∴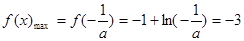 ,得
,得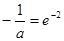 ,即
,即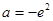 满足意题……3分
满足意题……3分
(2)由(1)知当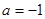 时,
时, ,所以
,所以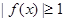 ………1分
………1分
又令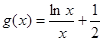 ,
,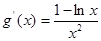 ,令
,令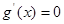 ,得
,得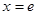
当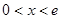 时,
时,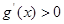 ,
,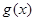 在
在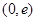 上单调递增;
上单调递增;
当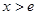 时,
时,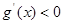 ,
,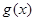 在
在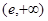 上单调递减;
上单调递减;
∴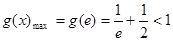 ,∴
,∴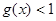 ,………4分
,………4分
∴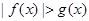 ,即
,即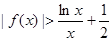
∴方程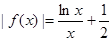 没有实数解.………1分
没有实数解.………1分
第二问中,利用由(1)知当
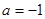 时,
时, ,所以
,所以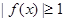
又令
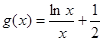 ,
,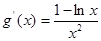 ,令
,令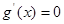 ,得
,得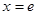
当
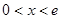 时,
时,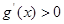 ,
,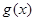 在
在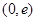 上单调递增;
上单调递增;当
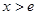 时,
时,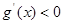 ,
,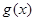 在
在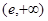 上单调递减;
上单调递减;∴
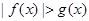 ,即
,即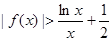
因此得到结论。
解:(1)
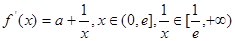 ………1分
………1分①若
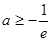 ,则
,则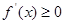 ,从而
,从而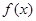 在
在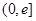 上是增函数,
上是增函数,∴
 ,不合题意………2分
,不合题意………2分②若
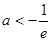 ,则由
,则由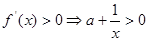 ,即
,即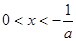 ,
,由
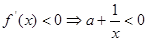 ,即
,即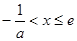
从而
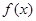 在
在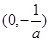 上是增函数,在
上是增函数,在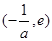 为减函数
为减函数∴
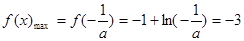 ,得
,得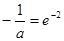 ,即
,即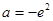 满足意题……3分
满足意题……3分(2)由(1)知当
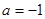 时,
时, ,所以
,所以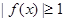 ………1分
………1分又令
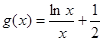 ,
,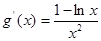 ,令
,令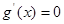 ,得
,得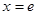
当
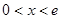 时,
时,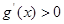 ,
,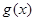 在
在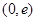 上单调递增;
上单调递增;当
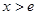 时,
时,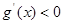 ,
,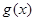 在
在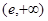 上单调递减;
上单调递减;∴
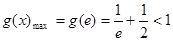 ,∴
,∴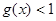 ,………4分
,………4分∴
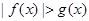 ,即
,即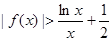
∴方程
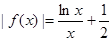 没有实数解.………1分
没有实数解.………1分
练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
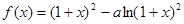 在
在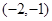 上是增函数,在
上是增函数,在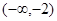 上为减函数.
上为减函数.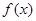 的表达式;
的表达式;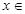
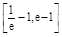 时,不等式
时,不等式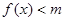 恒成立,求实数
恒成立,求实数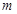 的值;
的值;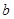 使得关于
使得关于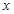 的方程
的方程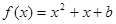 在区间[0,2]上恰好有两个相异的实根,若存在,求实数
在区间[0,2]上恰好有两个相异的实根,若存在,求实数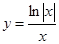 的图象大致是( )
的图象大致是( )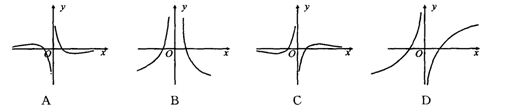
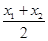 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由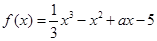 在区间
在区间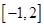 上不单调,则实数
上不单调,则实数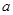 的取值范围是( ) .
的取值范围是( ) .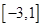
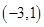
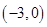
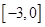
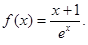
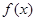 的单调区间;
的单调区间;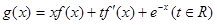 ,是否存在实数a、b、c∈[0,1],使得
,是否存在实数a、b、c∈[0,1],使得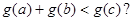 若存在,求出t的取值范围;若不存在,说明理由.
若存在,求出t的取值范围;若不存在,说明理由.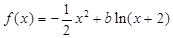 在
在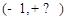 上是减函数,则b的取值范围是_____________
上是减函数,则b的取值范围是_____________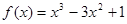 是减函数的区间为( )
是减函数的区间为( )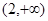
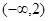
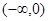
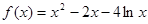 ,则
,则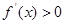 的解集为( )
的解集为( )