题目内容
14.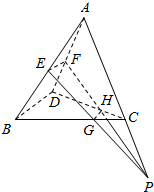 已知空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且$\frac{BG}{GC}=\frac{DH}{HC}$=2,求证:直线EG,FH,AC相交于同一点P.
已知空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且$\frac{BG}{GC}=\frac{DH}{HC}$=2,求证:直线EG,FH,AC相交于同一点P.
分析 由题意连接EF、HG、GE、FH、AC,根据比例关系和中位线证明出四边形EFHG是梯形,则由公理二得到直线EG,FH,AC相交于同一点P.
解答 证明:连接EF、HG、GE、FH、AC,如图,
∵BG:GC=DH:HC=2:1,
∴HG∥DB,且HG=$\frac{1}{3}$BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且EF=$\frac{1}{2}$BD,
∴四边形EFHG是梯形,∴EG与FH交于点P,
∵平面ABC∩平面ADC=AC,EG?平面ABC,FH?平面ADC,
∴由公理二得:直线EG,FH,AC相交于同一点P.
点评 本题考查了线线平行关系,主要根据平面几何中比例关系和中位线来证明线线平行,即平面几何中的知识在空间几何的一个平面内仍然适用

练习册系列答案
相关题目
4.若3$<(\frac{1}{3})$x<27,则( )
| A. | -1<<3 | B. | -3<<-1 | C. | x<-1或x>3 | D. | 1<x<3 |
7.已知四个函数y=3x,y=x2,y=3x,y=log3x,其中奇函数是( )
| A. | y=3x | B. | y=x2 | C. | y=3x | D. | y=log3x |