题目内容
【题目】已知函数f（x）是定义在[﹣3，0）∪（0，3]上的奇函数，当x∈（0，3]时，f（x）的图象如图所示，那么满足不等式f（x）≥2x﹣1 的x的取值范围是 ．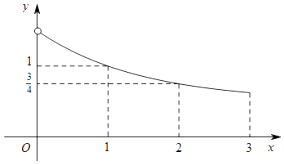 
【答案】[﹣3,﹣2]∪[0,1]
【解析】解：由图象可知，x=0时，2x﹣1=0，∴f（x）≥0，成立；
当x∈（0，3]时，f（x）单调递减，
当0＜x≤1时，f（x）＞1，2x﹣1≤1，满足不等式f（x）≥2x﹣1；
当1＜x＜3时，f（x）＜1，1＜2x﹣1＜7，不满足不等式f（x）≥2x﹣1；
∵函数f（x） 是定义在[﹣3，0）∪（0，3]上的奇函数，
∴当x∈[﹣3，0）时，f（x）单调递减，
当﹣3＜x≤﹣2时，﹣ 
≤f（x）＜0，﹣ 
＜2x﹣1≤﹣ ，满足不等式f（x）≥2x﹣1；
当x＞﹣2时，f（x）＜﹣ ，2x﹣1＞﹣ ，不满足不等式f（x）≥2x﹣1；
∴满足不等式f（x）≥2x﹣1 的x的取值范围是[﹣3，﹣2]∪[0，1]．
所以答案是：[﹣3，﹣2]∪[0，1]．
【考点精析】掌握函数的图象是解答本题的根本，需要知道函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
参考公式：b=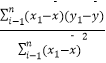 
= 
．
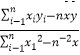（1）画出散点图；
（2）求回归直线方程；
（3）试预测广告费支出为10百万元时，销售额多大？
