题目内容
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以E的四个顶点为顶点的四边形的面积为4
,以E的四个顶点为顶点的四边形的面积为4 ![]() . (Ⅰ)求椭圆E的方程;
. (Ⅰ)求椭圆E的方程;
(Ⅱ)设A,B分别为椭圆E的左、右顶点,P是直线x=4上不同于点(4,0)的任意一点,若直线AP,BP分别与椭圆相交于异于A,B的点M、N,试探究,点B是否在以MN为直径的圆内?证明你的结论.
【答案】解:(Ⅰ)依题意得 ![]() =
= ![]() ,
, ![]() 2a2b=4
2a2b=4 ![]() ,又a2=b2+c2 , 由此解得a=2,b=
,又a2=b2+c2 , 由此解得a=2,b= ![]() . 所以椭圆E的方程为
. 所以椭圆E的方程为 ![]() =1.
=1.
(Ⅱ)点B在以MN为直径的圆内.证明如下:
方法1:由(Ⅰ)得A(﹣2,0),B(2,0).设M(x0 , y0).
∵M点在椭圆上,∴y02= ![]() (4﹣x02). ①
(4﹣x02). ①
又点M异于顶点A、B,∴﹣2<x0<2.
由P、A、M三点共线可以得P 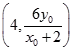 .
.
从而 ![]() =(x0﹣2,y0),
=(x0﹣2,y0), ![]() =
= 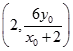 .
.
∴ ![]()
![]() =2x0﹣4+
=2x0﹣4+ ![]() =
= ![]() (x02﹣4+3y02). ②
(x02﹣4+3y02). ②
将①代入②,化简得 ![]()
![]() =
= ![]() (2﹣x0).
(2﹣x0).
∵2﹣x0>0,∴ ![]()
![]() >0,于是∠MBP为锐角,从而∠MBN为钝角,
>0,于是∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内.
方法2:由(Ⅰ)得A(﹣2,0),B(2,0).设M(x1 , y1),N(x2 , y2),
则﹣2<x1<2,﹣2<x2<2,又MN的中点Q的坐标为 ![]() ,
,
依题意,计算点B到圆心Q的距离与半径的差
|BQ|2﹣ ![]() |MN|2=
|MN|2= ![]() +
+ ![]() ﹣
﹣ ![]() [(x1﹣x2)2+(y1﹣y2)2]
[(x1﹣x2)2+(y1﹣y2)2]
=(x1﹣2)(x2﹣2)+y1y2 ③
直线AP的方程为y= ![]() (x+2),直线BP的方程为y=
(x+2),直线BP的方程为y= ![]() (x﹣2),
(x﹣2),
而两直线AP与BP的交点P在直线x=4上,
∴ ![]() =
= ![]() ,即y2=
,即y2= ![]() ④
④
又点M在椭圆上,则 ![]() =1,即y12=
=1,即y12= ![]() (4﹣x12) ⑤
(4﹣x12) ⑤
于是将④、⑤代入③,化简后可得|BQ|2﹣ ![]() |MN|2=
|MN|2= ![]() (2﹣x1)(x2﹣2)<0.
(2﹣x1)(x2﹣2)<0.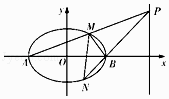
【解析】(Ⅰ)依题意得 ![]() =
= ![]() ,
, ![]() 2a2b=4
2a2b=4 ![]() ,又a2=b2+c2 , 由此解得a,b.即可得出.(Ⅱ)点B在以MN为直径的圆内.分析如下: 方法1:由(Ⅰ)得A(﹣2,0),B(2,0).设M(x0 , y0).又点M异于顶点A、B,可得﹣2<x0<2.由P、A、M三点共线可以得P.可得
,又a2=b2+c2 , 由此解得a,b.即可得出.(Ⅱ)点B在以MN为直径的圆内.分析如下: 方法1:由(Ⅰ)得A(﹣2,0),B(2,0).设M(x0 , y0).又点M异于顶点A、B,可得﹣2<x0<2.由P、A、M三点共线可以得P.可得 ![]()
![]() >0,即可证明.方法2:由(Ⅰ)得A(﹣2,0),B(2,0).设M(x1 , y1),N(x2 , y2),依题意,计算点B到圆心Q的距离与半径的差.|BQ|2﹣
>0,即可证明.方法2:由(Ⅰ)得A(﹣2,0),B(2,0).设M(x1 , y1),N(x2 , y2),依题意,计算点B到圆心Q的距离与半径的差.|BQ|2﹣ ![]() |MN|2=(x1﹣2)(x2﹣2)+y1y2 , 两直线AP与BP的交点P在直线x=4上,可得
|MN|2=(x1﹣2)(x2﹣2)+y1y2 , 两直线AP与BP的交点P在直线x=4上,可得 ![]() =
= ![]() ,化简后可得|BQ|2﹣
,化简后可得|BQ|2﹣ ![]() |MN|2<0,即可证明.
|MN|2<0,即可证明.