题目内容
【题目】有限数列![]() 同时满足下列两个条件:
同时满足下列两个条件:
①对于任意的![]() (
(![]() ),
),![]() ;
;
②对于任意的![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() 三个数中至少有一个数是数列
三个数中至少有一个数是数列![]() 中的项.[来
中的项.[来
(1)若![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)证明:![]() 不可能是数列
不可能是数列![]() 中的项;
中的项;
(3)求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 的最大值为
的最大值为![]()
【解析】
(1)由①,得![]() .
.
由②,当![]() ,
,![]() ,
,![]() 时.
时.![]() ,
,![]() ,
,![]() 中至少有一个是数列
中至少有一个是数列![]() ,
,![]() ,
,![]() ,
,![]() 中的项,但
中的项,但![]() ,
,![]() ,故
,故![]() ,解得
,解得![]() .
.
经检验,当![]() 时,符合题意.
时,符合题意.
(2)假设![]() 是数列
是数列![]() 中的项,由②可知:6,10,15中至少有一个是数列
中的项,由②可知:6,10,15中至少有一个是数列![]() 中的项,则有限数列
中的项,则有限数列![]() 的最后一项
的最后一项![]() ,且
,且![]() .
.
由①,![]() .
.
对于数![]() ,由②可知:
,由②可知:![]() ;对于数
;对于数![]() ,由②可知:
,由②可知:![]() . 6分
. 6分
所以![]() ,这与①矛盾.
,这与①矛盾.
所以![]() 不可能是数列
不可能是数列![]() 中的项.
中的项.
(3)![]() 的最大值为
的最大值为![]() ,证明如下:
,证明如下:
(1)令![]() ,则
,则![]() 符合①、②.
符合①、②.
(2)设![]() 符合①、②,则:
符合①、②,则:
(ⅰ)![]() 中至多有三项,其绝对值大于1.
中至多有三项,其绝对值大于1.
假设![]() 中至少有四项,其绝对值大于1,不妨设
中至少有四项,其绝对值大于1,不妨设![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中绝对值最大的四项,其中
中绝对值最大的四项,其中![]() .
.
则对![]() ,
,![]() ,
,![]() 有
有![]() ,
,![]() ,故
,故![]() ,
,![]() 均不是数列
均不是数列![]() 中的项,即
中的项,即![]() 是数列
是数列![]() 中的项.
中的项.
同理:![]() 也是数列
也是数列![]() 中的项.
中的项.
但![]() ,
,![]() .
.
所以![]() .
.
所以![]() ,这与①矛盾.
,这与①矛盾.
(ⅱ)![]() 中至多有三项,其绝对值大于0且小于1.
中至多有三项,其绝对值大于0且小于1.
假设![]() 中至少有四项,其绝对值大于0且小于1,类似(ⅰ)得出矛盾.
中至少有四项,其绝对值大于0且小于1,类似(ⅰ)得出矛盾.
(ⅲ)![]() 中至多有两项绝对值等于1.
中至多有两项绝对值等于1.
(ⅳ)![]() 中至多有一项等于0.
中至多有一项等于0.
综合(ⅰ),(ⅱ),(ⅲ),(ⅳ)可知![]() 中至多有9项.
中至多有9项.
14分
由(1),(2)可得,![]() 的最大值为9.
的最大值为9.

 名校课堂系列答案
名校课堂系列答案【题目】某商场营销人员对某商品![]() 进行市场营销调查,发现每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到下表:
进行市场营销调查,发现每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到下表:
回馈点数 | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析发现,可用线性回归模型拟合该商品每天的销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若回馈6个点时该商品每天销量;
,并预测若回馈6个点时该商品每天销量;
(2)已知节日期间某地拟购买该商品的消费群体十分庞大,营销调研机构对其中的200名消费者的返点数额的心理预期值进行了抽样调查,得到如下频数表:
返还点数预期值区间 |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位拟购买该商品的消费者对返点点数的心理预期值的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0.1);
(ii)将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望紧缩型”消费者的人数为随机变量
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望紧缩型”消费者的人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式及数据:①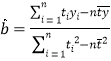 ,
,![]() ;②
;②![]() .
.