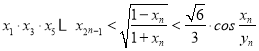题目内容
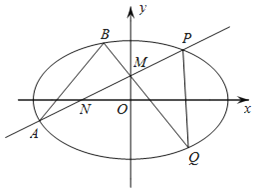
【题目】已知椭圆E:![]() ,点A,B分别是椭圆E的左顶点和上顶点,直线AB与圆C:x2+y2=c2相离,其中c是椭圆的半焦距,P是直线AB上一动点,过点P作圆C的两条切线,切点分别为M,N,若存在点P使得△PMN是等腰直角三角形,则椭圆离心率平方e2的取值范围是_____.
,点A,B分别是椭圆E的左顶点和上顶点,直线AB与圆C:x2+y2=c2相离,其中c是椭圆的半焦距,P是直线AB上一动点,过点P作圆C的两条切线,切点分别为M,N,若存在点P使得△PMN是等腰直角三角形,则椭圆离心率平方e2的取值范围是_____.
【答案】[![]() ,
,![]() ).
).
【解析】
根据直线和圆相离得到a2b2>c2(a2+b2),根据等腰三角形得到2e4﹣5e2+1≤0,计算得到答案.
AB所在直线方程为![]() ,即bx﹣ay+ab=0,
,即bx﹣ay+ab=0,
又直线AB与圆C:x2+y2=c2相离,∴![]() c,
c,
即a2b2>c2(a2+b2),∴a2(a2﹣c2)>c2(2a2﹣c2),
整理得:e4﹣3e2+1>0,解得0<e2![]() ;
;
又存在点P使得△PMN是等腰直角三角形,
则在Rt△OPN中,OP![]() ON
ON![]() c,
c,
∴![]() ,即a2b2≤2c2(a2+b2),
,即a2b2≤2c2(a2+b2),
∴a2(a2﹣c2)≤2c2(2a2﹣c2),
整理得2e4﹣5e2+1≤0,解得![]() e2<1.
e2<1.
∴e2的取值范围是[![]() ,
,![]() ).
).
故答案为:[![]() ,
,![]() ).
).


练习册系列答案
相关题目