题目内容
12. 已知中心在原点,焦点在x轴上的椭圆C过点P(0,$\sqrt{3}$),离心率e=$\frac{1}{2}$.
已知中心在原点,焦点在x轴上的椭圆C过点P(0,$\sqrt{3}$),离心率e=$\frac{1}{2}$.(1)求椭圆C的方程
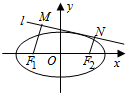
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点.
①求k,m满足的关系式
②如图,F1,F2为椭圆的左右焦点,作F1M⊥l,F2N⊥l,垂足分别为M,N,四边形F1MNF2的面积S是否存在最大值?若存在,求出该最大值,若不存在请说明理由.
分析 (1)椭圆C过点P(0,$\sqrt{3}$),离心率e=$\frac{1}{2}$.可求得椭圆方程.
(2)设出直线方程代入椭圆列式得到关系式,根据面积公式,由均值不等式求得最值.
解答 解:(1)设椭圆得方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,∴$b=\sqrt{3},c=1$.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)①将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中,
得(4k2+3)x2+8kmx+4m2-12=0,由直线l与椭圆C仅有一个公共点知,
△=64k2m2-4(4k2+3)(4m2-12)=0,化简得m2=4k2+3,
②设d1=|F1M|=$\frac{|-k+m|}{\sqrt{{k}^{2}+1}},{d}_{2}=|{F}_{2}M|=\frac{|k+m|}{\sqrt{{k}^{2}+1}}$当k≠0时,设直线l的倾斜角为θ.
则|d1d2|=|MN||tanθ|,∴$|MN|=|\frac{{d}_{1}-{d}_{2}}{k}|$,
$S=\frac{1}{2}|\frac{{d}_{1}-{d}_{2}}{k}|({d}_{1}+{d}_{2})=|\frac{{d}_{1}^{2}-{d}_{2}^{2}}{2k}|$=$\frac{2|m|}{{k}^{2}+1}=\frac{2|m|}{\frac{{m}^{2}-3}{4}+1}=\frac{8}{|m|+\frac{1}{|m|}}$,
∵m2=4k2+3,当k≠0时,$|m|>\sqrt{3},|m|+\frac{1}{|m|}>\sqrt{3}+\frac{1}{\sqrt{3}}=\frac{4\sqrt{3}}{3}$,
∴$S<2\sqrt{3}$又当k=0时,四边形F1MNF2为矩形,$S=2\sqrt{3}$,
∴四边形F1MNF2的最大值为$S=2\sqrt{3}$.
点评 本题主要考查直线与圆锥曲线的关系,利用均值不等式求得最值.在高考中圆锥曲线的最值经常与均值不等式合体考查,应重点注意.

| A. | ($\frac{1}{3}$,$\frac{3}{4}$) | B. | ($\frac{3}{4}$,$\frac{5}{2}$) | C. | ($\frac{1}{3}$,$\frac{5}{2}$) | D. | ($\frac{5}{4}$,$\frac{5}{2}$) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,O为坐标原点,点B在C上,△OBA为等腰直角三角形.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,O为坐标原点,点B在C上,△OBA为等腰直角三角形. 如框图,当x1=6,x2=9,p=8.5时,x3=8.
如框图,当x1=6,x2=9,p=8.5时,x3=8.