题目内容
2.假设随机变量X的绝对值不大于1,P{X=-1}=$\frac{1}{8}$,P{X=1}|=$\frac{1}{4}$;在事件{-1<X<1}出现的条件下,X在(-1,1)内的任一子区间上取值的条件概率与该子区间的长度成正比,试求:(1)X的分布函数F(x);
(2)X取负值的概率p.
分析 (1)x<-1时,F(x)=0,x≥1,F(x)=1,再求出F(x)=P(X≤-1)+P{-1<X≤x}=$\frac{1}{16}$(5x+7),即可得到X的分布函数F(x);
(2)X取负值的概率P(X≤0)=F(0).
解答 解:(1)由题设知,x<-1时,F(x)=0,F(-1)=$\frac{1}{8}$,
∴P{-1<X≤1}=1-$\frac{1}{8}$-$\frac{1}{4}$=$\frac{5}{8}$,
P{-1<X≤x|-1<X<1}=$\frac{1}{2}$(x+1)(|x|<1),
∴P{-1<X≤x}=$\frac{5}{8}•\frac{x+1}{2}$=$\frac{5(x+1)}{16}$,
∴F(x)=P(X≤-1)+P{-1<X≤x}=$\frac{1}{16}$(5x+7),
∵x≥1,F(x)=1,
∴F(x)=$\left\{\begin{array}{l}{0,x<-1}\\{\frac{1}{16}(5x+7),-1≤x<1}\\{1,x≥1}\end{array}\right.$;
(2)P=P(X≤0)=F(0)=$\frac{7}{16}$.
点评 本题考查分布函数,考查概率的计算,考查学生分析解决问题的能力,正确求出概率是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在区间[-1,5]上任取一个数x,则log2(x+3)≥log2(3x+4)-1的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
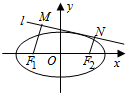 已知中心在原点,焦点在x轴上的椭圆C过点P(0,$\sqrt{3}$),离心率e=$\frac{1}{2}$.
已知中心在原点,焦点在x轴上的椭圆C过点P(0,$\sqrt{3}$),离心率e=$\frac{1}{2}$.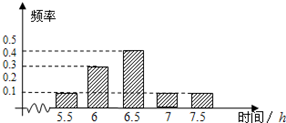 某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.
某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示. 如图,△ABC内接于圆O,直线L平行AC交线段BC于D,交线段AB于E,交圆O于G、F,交圆O在点A的切线于P.若D是BC的中点,PE=6,ED=4,EF=6,则PA的长为2$\sqrt{6}$.
如图,△ABC内接于圆O,直线L平行AC交线段BC于D,交线段AB于E,交圆O于G、F,交圆O在点A的切线于P.若D是BC的中点,PE=6,ED=4,EF=6,则PA的长为2$\sqrt{6}$.