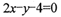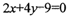题目内容
．（12分）（理）抛物线y=ax2＋bx在第一象限内与直线x＋y=4相切．此抛物线与x轴所围成的图形的面积记为S．求使S达到最大值的a、b值，并求Smax．
（理）解：依题设可知抛物线为凸形，它与x轴的交点的横坐标分别为x1=0，x2=－b/a，所以
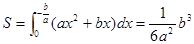(1)
又直线x＋y=4与抛物线y=ax2＋bx相切，即它们有唯一的公共点，
由方程组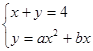
得ax2＋(b＋1)x－4=0，其判别式必须为0，即(b＋1)2＋16a=0．
于是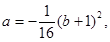
代入（1）式得：
，
；
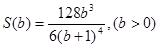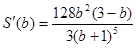令S'(b)=0；在b＞0时得唯一驻点b=3，且当0＜b＜3时，S'(b)＞0；当b＞3时，S'(b)＜0．故
在b=3时，S(b)取得极大值，也是最大值，即a=－1，b=3时，S取得最大值，且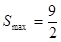
。
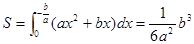(1)又直线x＋y=4与抛物线y=ax2＋bx相切，即它们有唯一的公共点，
由方程组
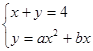
得ax2＋(b＋1)x－4=0，其判别式必须为0，即(b＋1)2＋16a=0．
于是
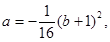代入（1）式得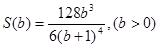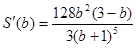：，； 令S'(b)=0；在b＞0时得唯一驻点b=3，且当0＜b＜3时，S'(b)＞0；当b＞3时，S'(b)＜0．故
在b=3时，S(b)取得极大值，也是最大值，即a=－1，b=3时，S取得最大值，且
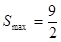。略
练习册系列答案
相关题目
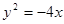的焦点为F，其准线与x轴交于点M，过点M作斜率为k的直线l交抛物线于A、B两点，.
O），求证：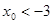
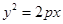的通径是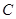
的方程为
，
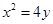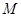为直线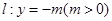
上任意一点，过点
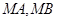，切点分别为
,
.
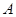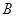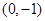时，求过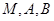
三点的圆的方程，并判断直线
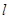与此圆的位置关系； 
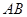恒过定点；
变化时，试探究直线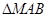
为直角三角形，若存在，有几个这样的点，若不存在，说明理由.
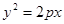的焦点与双曲线
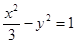的右焦点重合，则p的值为（）
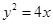上，则该点到点
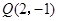的距离与到抛物线焦点距离之和取得最小值时的坐标为（ ）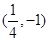
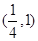
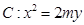
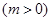和直线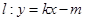
没有公共点（其中
、
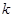为常数），动点
是直线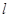
上的任意一点，过
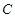的两条切线，切点分别为
、
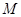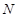，且直线
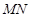恒过点
.
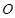点为原点，连结
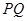交抛物线
、
两点，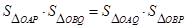
.
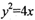交于A,B两点;线段AB中点为
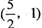，则直线l的方程为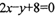
、
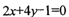