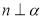题目内容
3.已知数列{an}中,a1=1,(n+1)an=nan+1,则数列{an}的通项公式an=n.分析 通过变形可知$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,累乘计算即得结论.
解答 解:∵(n+1)an=nan+1,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n}{n-1}$,$\frac{{a}_{n-1}}{{a}_{n-2}}$=$\frac{n-1}{n-2}$,…,$\frac{{a}_{2}}{{a}_{1}}$=$\frac{2}{1}$,
累乘得:$\frac{{a}_{n}}{{a}_{1}}$=$\frac{n}{1}$,
又∵a1=1,
∴an=n,
故答案为:n.
点评 本题考查数列的通项,利用累乘法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知α为第三象限角,则tan$\frac{α}{2}$的值( )
| A. | 一定为正数 | B. | 一定为负数 | ||
| C. | 可能为正数,也可能为负数 | D. | 不存在 |
15.不等式2+log0.5(5-x)+log2$\frac{1}{x}$>0的解集是( )
| A. | (0,+∞) | B. | (-∞,5) | C. | (0,1)∪(4,5) | D. | 空集 |
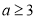 ,函数
,函数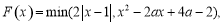 其中
其中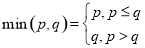 .
. 成立的
成立的 的取值范围;
的取值范围; 的最小值
的最小值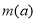 ;
;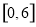 上的最大值
上的最大值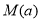 .
.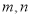 表示两条不同直线,
表示两条不同直线,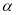 表示平面.下列说法正确的是
表示平面.下列说法正确的是 则
则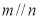 B.若
B.若 ,则
,则
 则
则 D.若
D.若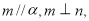 ,则
,则