题目内容
14.已知等差数列{an}的前三项分别为a,b,a+b,等比数列{bn}的前三项分别为a,b,ab,那么数列{$\frac{{a}_{n}}{2{b}_{n}}$}的前n项和为2-$\frac{2+n}{{2}^{n}}$.分析 利用等差数列与等比数列的通项公式可得a,b,an,bn,再利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:∵等差数列{an}的前三项分别为a,b,a+b,
∴等差数列{an}的公差d=b+a-b=a.
∴an=a+(n-1)a=na.
∵等比数列{bn}的前三项分别为a,b,ab,
∴等比数列{bn}的公比q=$\frac{ab}{b}$=a,
∴bn=an.
联立$\left\{\begin{array}{l}{b=2a}\\{b={a}^{2}}\end{array}\right.$,a≠0,解得a=2,b=4.
∴$\frac{{a}_{n}}{2{b}_{n}}$=$\frac{na}{2{a}^{n}}$=$\frac{1}{2}•\frac{n}{{a}^{n-1}}$=$\frac{n}{{2}^{n}}$.
∴数列{$\frac{{a}_{n}}{2{b}_{n}}$}的前n项和Sn=$\frac{1}{2}+\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,
$\frac{1}{2}{S}_{n}$=$\frac{1}{{2}^{2}}$+$\frac{2}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n}}$+$\frac{n}{{2}^{n+1}}$,
∴$\frac{1}{2}{S}_{n}$=$\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$=1-$\frac{2+n}{{2}^{n+1}}$,
∴Sn=2-$\frac{2+n}{{2}^{n}}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2) | C. | (2,+∞) | D. | (-∞,0) |
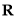 上的函数
上的函数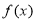 满足
满足 且
且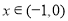 时,
时,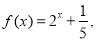 则
则 __________.
__________. (
( ),若无论
),若无论 为何值,函数
为何值,函数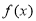 的图象总是一条直线,则
的图象总是一条直线,则 的值是
的值是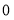 B.
B.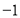 C.4 D.256
C.4 D.256 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过 的直线交椭圆于A、B两点若
的直线交椭圆于A、B两点若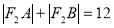 ,则
,则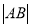 =_____.
=_____.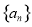 满足
满足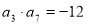 ,
,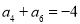 ,求数列
,求数列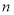 项和Sn
项和Sn