题目内容
8．若x＜0，则ln（x+1）＜0的否命题是若x≥0，则ln（x+1）≥0．分析 根据已知中的原命题，结合否命题的定义，可得答案．
解答 解：∵原命题为：若x＜0，则ln（x+1）＜0，
∴否命题为：若x≥0，则ln（x+1）≥0，
故答案为：若x≥0，则ln（x+1）≥0．
点评 本题考查的知识点是四种命题，难度不大，属于基础题．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
18．若关于实数x的不等式|x-5|+|x+3|＜a无解，则实数a的取值范围是（ ）
| A． | （-∞，8] | B． | （-∞，8） | C． | （8，+∞） | D． | [8，+∞） |
16．
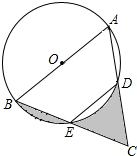如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和为（ ）
如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 1 |
13．以模型y=cekx去拟合一组数据时，为了求出回归方程，设z=lny，其变换后得到线性回归方程z=0.3x+4，则c=（ ）
| A． | 0.3 | B． | e0.3 | C． | 4 | D． | e4 |
如图，一艘轮船按照北偏西30°的方向以每小时30海里的速度从A处开始航行，此时灯塔M在轮船的北偏东45°方向上，经过40分钟后，轮船到达B处，灯塔在轮船的东偏南15°方向上，则灯塔M和轮船起始位置A的距离为$\frac{20\sqrt{6}}{3}$海里．
18．己知函数f（x）=（x-l）（log3a）2-6（log3a）x+x+l在x∈[0，l]内恒为正值，则a的取值范围是（ ）
| A． | -1＜a＜$\frac{1}{3}$ | B． | a＜$\frac{1}{3}$ | C． | a＞$\root{3}{3}$ | D． | $\frac{1}{3}$＜a＜$\root{3}{3}$ |