题目内容
【题目】已知在锐角![]() 中,角
中,角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,且
,且![]()
(1)求角![]() 大小;
大小;
(2)当![]() 时,求
时,求![]() 的取值范围。
的取值范围。
【答案】(1)由已知及余弦定理,得![]() 因为
因为![]() 为锐角,所以
为锐角,所以![]()
(2)由正弦定理,得![]() ,
,
![]()
![]()
![]()
由![]() 得
得![]()
![]()
![]()
【解析】
试题分析:(I)利用锐角△ABC中,sinC=![]() ,求出角C的大小;(II)先求得 B+A=150°,根据B、A都是锐角求出A的范围,由正弦定理得到a=2sinA,b=2sinB=2sin(A+30°),根据 a2+b2=4+2
,求出角C的大小;(II)先求得 B+A=150°,根据B、A都是锐角求出A的范围,由正弦定理得到a=2sinA,b=2sinB=2sin(A+30°),根据 a2+b2=4+2![]() sin(2A﹣60°) 及A的范围,得(2A﹣60°),从而得到a2+b2的范围.
sin(2A﹣60°) 及A的范围,得(2A﹣60°),从而得到a2+b2的范围.
详解:(I)由已知及余弦定理,得tanC=![]() =
=![]() =
=![]() ,
,
∴sinC=![]() ,故锐角C=
,故锐角C=![]() .
.
(II)当C=1时,∵B+A=150°,∴B=150°﹣A.由题意得![]() ,
,
∴60°<A<90°.由 ![]() =2,得 a=2sinA,b=2sinB=2sin(A+30°),
=2,得 a=2sinA,b=2sinB=2sin(A+30°),
∴a2+b2=4[sin2A+sin2(A+30°)]=4[![]() +
+![]() ]=4[1﹣
]=4[1﹣![]() cos2A﹣
cos2A﹣![]() (
(![]() cosA﹣
cosA﹣![]() sin2A)]=4+2
sin2A)]=4+2![]() sin(2A﹣60°).
sin(2A﹣60°).
∵60°<A<90°,∴(2A﹣60°).
∴7<a2+b2≤4+2![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 |
|
|
|
|
|
|
|
年利润增长 |
|
|
|
|
|
|
|
(1)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额为
的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额为![]() 万元,估计该公司在该年的年利润增长为多少?(结果保留两位小数)
万元,估计该公司在该年的年利润增长为多少?(结果保留两位小数)
(2)现从2012年—2018年这![]() 年中抽出三年进行调查,记
年中抽出三年进行调查,记![]() 年利润增长
年利润增长![]() 投资金额,设这三年中
投资金额,设这三年中![]() (万元)的年份数为
(万元)的年份数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考公式: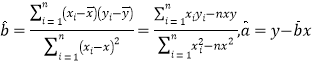 .
.
参考数据:![]() ,
,![]() .
.